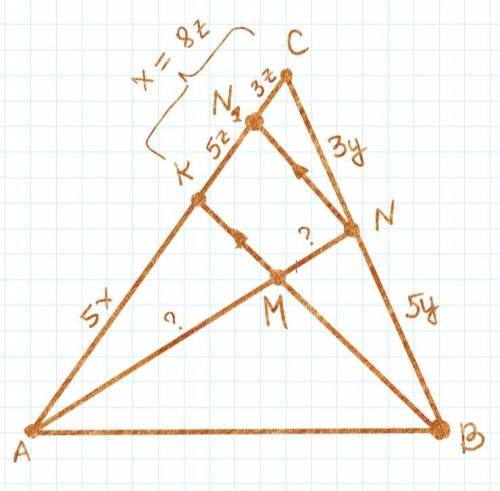
Задание 1.
во вложениях
Задание 2.
Пусть 3х - яблонь в саду, тогда х - груш.
По условию задачи, когда вырубили 14 яблонь и посадили 10 груш, деревьев стало поровну.
Составим и решим уравнение:
3х - 14 = х + 10
3х - х = 10 + 14
2х = 24
х = 12 - количество груш в саду
Т. к. по условию задачи яблонь в 3 раза больше, чем груш, то:
12 × 3 = 36 - количество яблонь в саду
ответ: 12 груш и 36 яблонь.
Задание 3.
а) 3( х + 0,6) = 3 - х
3х + 1,8 = 3 - х
3х + х = 3 - 1,8
4х = 1,2
х = 0,3
ответ: 0,3.
б) во вложениях
Задание 4.
2,5 : 8,75 = х : 21
х = 2,5 × 21 ÷ 8,75
х = 6
ответ: 6.
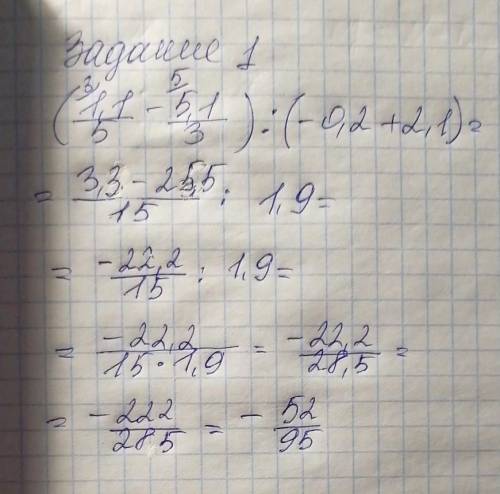

Замечание:
В условии опечатка AF ÷ FC = 5 следует читать как AK ÷ KC
Дано:
ΔABC
AK ÷ KC = 5 ÷ 1
CN ÷ NB = 3 ÷ 5 (так как 0,6 = 3/5)
AN ∩ BK = M
Найти:
SΔAMB ÷ SΔMBN - ?
Дополнительное построение: NN₁ ║ BK (см. рисунок)
В ΔBCK:
CN₁ ÷ N₁K = CN ÷ NB (обобщенная теорема Фалеса) = 3 ÷ 5; CN = 3y; NB = 5y; CB = 8y; CN₁ = 3z; N₁K = 5z; CK = 8z; AK ÷ CK = 5 ÷ 1; AK = 5x; CK = x
поэтому 8z = x ⇒ z = 1/8 x. В итоге получаем: N₁K = 5/8 x
В ΔAN₁N: AK ÷ KN₁ = AM ÷ MN (обобщенная теорема Фалеса), поэтому
AM ÷ MN = 5x ÷ (5/8 x) = 8 ÷ 1
SΔAMB ÷ SΔMBN = AM ÷ MN (отношение площадей треугольников с общей высотой) = 8 ÷ 1