Площа азовського моря близько 38000 км², що складає 19/210 від прощі чорного моря. знайди площу чорного моря.

👇

Увидеть ответ

Ответ:

evazorina1

18.11.2022

Пошаговое объяснение:

38000 : 19/210=38000*210/19=2000*210=420000 км²

4,8(48 оценок)

Ответ:

tony23

18.11.2022

38000:(19/210)=38000*(210/19)=(38000*210)/19= сократим на 19

2000*210=420 000 км² - это площадь Черного моря.

Нахождение целого по известной части (дроби).

4,4(69 оценок)

Открыть все ответы

Ответ:

Killer3D

18.11.2022

10000:100·15=1500 р. - проценты по вкладу к концу первого года
10000+1500=11500 р - сумма вклада к концу первого года
Пусть вкладчик положил х р. в конце первого года
Тогда сумма вклада на начало второго составила (11500+х) р.
(11500+х):100·15=0,15(11500+х) - проценты по вкладу к концу второго года
(11500+х) + 0,15(11500+х)=1,15·(11500+х) - сумма вклада к концу второго года.
По условию, эта сумма на 475% больше по сравнению с первоначальным вкладом
или
10 000: 100·475=47500 р
Составляем уравнение
1,15·(11500+х) - 47500=10000
1,15х=54275
х=38500
ответ. 38500 р.

Проверка
11500+38500=50000 р - сумма вклада на начало 2 года
50000:100·15=7500 р - проценты по вкладу к концу 2 года
57500 р - сумма вклада к концу 2 года
57500-10000=47500 р на такую сумму увеличился первоначальный вклад ( за счет % и внесенной суммы)
47500 составляют 475 % от 10 000

4,7(37 оценок)

Ответ:

tar02

18.11.2022

Это уравнение является уравнением Бернулли.
Очевидно, что функция y = 0

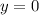является решением уравнения. Разделим обе части на y^2

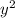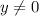, предполагая, что $y \neq 0$ :
$(1+x^2) \frac{y'}{y^2} + \frac{1}{y} = arctgx$ .
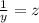Сделаем замену $\frac{1}{y} = z$ , тогда 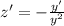$z' = -\frac{y'}{y^2}$ и уравнение принимает вид
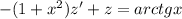-(1+x^2)z' + z = arctgx

.
Получили линейное неоднородное уравнение. Решим его методом вариации постоянной. Для этого найдем решение соответствующего однородного уравнения:
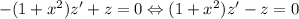$-(1+x^2)z' + z = 0 \Leftrightarrow (1+x^2)z' - z = 0$ .
Это уравнение с разделяющимися переменными.
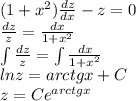$(1+x^2) \frac{dz}{dx} - z = 0 \\ \frac{dz}{z} = \frac{dx}{1+x^2} \\ \int \frac{dz}{z} = \int \frac{dx}{1+x^2} \\ lnz = arctgx + C \\ z = Ce^{arctgx}$ .
Заменим постоянную C новой неизвестной функцией C(x) и в таком виде будем искать решение неоднородного уравнения:
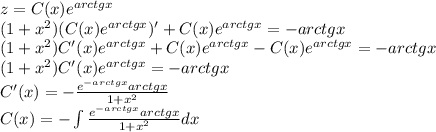$z = C(x)e^{arctgx} \\ (1+x^2)(C(x)e^{arctgx})' + C(x)e^{arctgx} = -arctgx \\ (1+x^2)C'(x)e^{arctgx} + C(x)e^{arctgx} - C(x)e^{arctgx} = -arctgx \\ (1+x^2)C'(x)e^{arctgx} = -arctgx \\ C'(x)=-\frac{e^{-arctgx}arctgx}{1+x^2} \\ C(x) = -\int\frac{e^{-arctgx}arctgx}{1+x^2}dx$ .
Сделаем замену в интеграле:
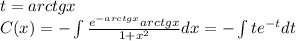$t = arctgx\\ C(x) =-\int\frac{e^{-arctgx}arctgx}{1+x^2}dx = -\int te^{-t}dt$ .
Интеграл легко берется по частям (оставляю на вас):
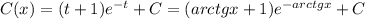$C(x) = (t+1)e^{-t} + C = (arctgx+1)e^{-arctgx} + C$ , где C - произвольная постоянная.
Таким образом,
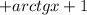$z = C(x)e^{arctgx} = ((arctgx+1)e^{-arctgx} + C)e^{arctgx} = Ce^{arctgx}$ +arctgx + 1

.
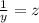Вспоминаем, что $\frac{1}{y} = z$ , тогда
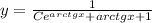$y = \frac{1}{Ce^{arctgx}+arctgx+1}$ - общее решение.
Теперь воспользуемся начальным условием y(0) = 1:
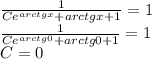$\frac{1}{Ce^{arctgx} + arctgx + 1} = 1\\ \frac{1}{Ce^{arctg0} + arctg0 + 1} = 1 \\ C = 0$ .
Значит, искомая функция есть
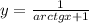$y = \frac{1}{arctgx + 1}$ .