1. диаметр D=2*R=2*6=12(cм)
2. Осевое сечение цилиндра - это прямоугольник, у которого одна сторона (диаметр) равна 12 см, вторая (высота) - 6 см. Диагональ осевого сечения - гипотенуза прямоугольного треугольника (который получается, если провести диагональ) со сторонами 12 см и 6 см. По теореме Пифагора имеем, что диагональ равна корень(12^2+6^2)=корень(144+36)=корень(180)=6*корень(5) (см).
3. Тангенс угла наклона диагонали диагонали к плоскости основания по определению равен отношению противолежажего катета к прилежащему, т. е. tg A=высота:диаметр=6/12=1/2, откуда угол А=arctg(1/2).
4. Площадь основания цилиндра - это площадь круга радиуса R=6 см, которая вычисляется по формуле:S=Пи* R^2=Пи*6^2=Пи*36=3,14*36=113,04 (см кв.)
5. Площадь осевого сечения - это площадь прямоугольника со сторонами 12 см и 6 см (см. объяснение в п. 2), т. е. S=12*6=72 (см кв.)
6. Длина окружности основания цилиндра : С=2*Пи*R=2*Пи*6=12Пи= 36,68(см)
1. Длина окружности может быть определена по формуле:
C = π*d = 3,14*35 = 109,9 см
где d – диаметр.
2. Масштаб 1:1000 подразумевает, что на карте все линейные размеры уменьшены в 1000 раз по сравнению с реальными. Отсюда:
L = 9,6*1000 = 9600 см или 96 м
3. Площадь круга может быть определена по формуле
S = π*r^2 = π*7^2 = 3,1*49 = 151.9 дм^2
где r – радиус.
4. Процент снижения цены товара определится:
p = 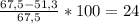
5. Площадь прямоугольника определяется по формуле:
S = a*b
где a, b – стороны.
Каждая сторона в 500 раз больше, чем на плане (см. задачу 2), таким образом, реальная площадь прямоугольного участка:
Sр = 500*a*500*b = 250000*S = 250000*25 = 6250000 см^2 или 625 м^2