1)в 250 кг сахарной свеклы содержится 45 кг сахара.сколько процентов составляет содержание сахара в сахарной свекле? 2)после сушки 50 кг свежего чернослива получили 18 кг сушеного.сколько проценттов составляет масса сушеного чернослива от массы свежего? 3)в 450 кг руды содержится 67,5 кг меди.сколько процентов меди содержится в руде?
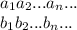
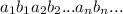
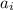 равен 2i-1
равен 2i-1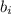 равен 2i
равен 2i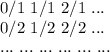

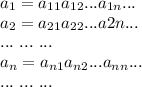
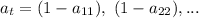
9/50=0.18=18℅
2)28:50=0.36
0.36•100=36℅
3)450:100=4.5кг(это 1℅)
66.5:4.5=15%