Путь х см - искомая ширина прямоугольника, занесём данные из условия задачи в таблицу:
Изначально Предположение
ширина х см (х+15) см
длинна (х+10) см (х+10+20) см
Площадь х(х+10) кв см (х+15)(х+30) кв см
По условию задачи составляем уравнение:
5х(х+10) = (х+15)(х+30)
5х²+50х = х²+30х+15х+450
5х²+50х = х²+45х+450
4х² + 5 х - 450 = 0
Д = 25+16*450 = 7225=85²
х(1) = (-5+85) / 8 = 10
х(2) = (-5-85) / 8 < 0 не подходит под условие задачи, ибо ширина >0
ответ: искомая ширина прямоугольника 10 см
Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену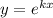 
.
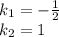
Общее решение однородного диф. уравнения: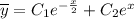 
.
Рассмотрим функцию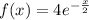 
. Здесь 
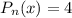, где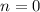 
, 
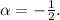Сравнивая 
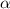с корнями характеристического уравнения и принимая во внимая, что
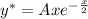
Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на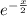 
.
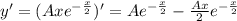
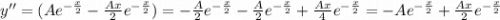
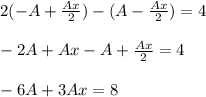
Приравниваем коэффициенты при степенях x
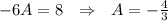
Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения
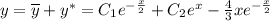
ответ: 25.