1. В 1 очередь надо найти область определения
Для левой части это будет x ≠ 2, ее же в этом случае приведем к виду
log√3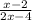
=log√3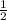
В правой части область определения x ≠ 2 и (x+1)/(x+2)>0, если x+1 >0 то и подавно x+2>0, если х+1 < 0 и x+2 <0, то x< -2, тогда x∈(-∞,-2)∪(-1,+∞), но с учетом x ≠2 имеем область определения x∈(-∞,-2)∪(-1,2)∪(2,+∞)
Теперь, избавляясь от логоарифмов
1/2= (x+1)/(x+2), x+2=2x+2
x =0
2. Тоже сначала ищем область определения
x²-9 ≥0, x ∈(-∞,-3]∪[3,+∞)
x+3 ≥ 0, x ∈ [-3,+∞)
x²+6x+9=(x+3)²≥0 ∀ x
Область определения в этом случае имеет вид x ∈ [3,+∞)
тогда имеем уравнение
+ 
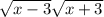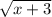≥x+3
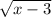+1 ≥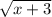
x-3+2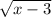+1≥x+3
2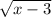≥5
x-3 ≥ 6,25
x ≥ 9,25
3. x=2y
x-y=y, x-y+1=y+1
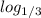4y +
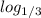4y=0
4y=1,
y=0,25, x=0,5
Пошаговое объяснение:
1)0,02
2)0.6×16 = 9.6 км катер против течения
16.8 - 9.6 =7.2 км по течению
7.2 / 0.4=18 км/ч - скорость по течению
ответ:18,
3)7,2х - 5,4х + 0,55 = 1
1,2х + 0,55= 1
1,2х = 1 - 0,55
1,2х = 0,45
х = 0,45 : 1,2
х = 0,375
4)Пусть х см - длина пар-да,тогда
х см - 1
3,6 см - 9/25
х=3,6: 9/25=36/10 ·25/9=10см - длина пар-да
0,42·10=4,2 см - высота
V=abc=3,6·10·4,2=151,2 см³
5)1)17 16/19-5 16/19=(17-5)+(16/19-16/19)=12 0/19=228/19=12
2)7 3/5-4 4/5=(7-4)+(3/5-4/5)=-3 1/5
3)30:12 =30/1:12/1=30/1*1/12=30/12=2 6/12
4)-3 1/5:7=-16/5:7/1=-16/5*1/7=-16/36
5)2 6/12-16/36=2 2/36
6)сумма трех чисел = среднее арифметическое*количество чисел = 2,5*3=7,5
сумма двух чисел = среднее арифметическое*количество чисел = 1,7*2=3,4
сумма пяти чисел = 7,5+3,4=10,9
среднее = 10,9/5=2ц 9/50
Пошаговое объяснение:
119 на простые множители 7 17
В 136 есть простой множитель 17 и в 119 есть простой множитель 17, значит 136 и 119 не взаимно простые.