ответ: 180.
Вот формула площади трапеции:
, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).
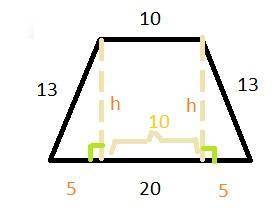
Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен 
. Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:
Теперь высоту мы знаем и можем найти площадь трапеции:
Задача решена!
1) скобка:
в/а(9-а²) - 1/а(а+3) - 3/в(9-а²)=
(в*в-1*в(3-а)-3а)/ав(9-а²)=
(в²-3в+ав-3а)/ав(9-а²)=(в²+ав-3в-3а)/ав(9-а²)=
(в(в+а)-3(в+а))/ав(9-а²)=(в+а)(в-3)/ав(9-а)²
2) деление:
(в+а)(в-3)/ав(9-а²) : (в-3)²/ав(а²-9)=
(в+а)(3-в)/[ав(а²-9)] * [ав(а²-9)]/(3-в)²= сократим квадр. скобки
(а+в)(3-в)/(3-в)²=(а+в)/(3-в)=(3+2)/(3-2)=5.