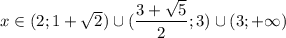984
Пошаговое объяснение:
Самое большое трёхзначное число равно 999. Но, в в задании есть условие, что цифры числа должны быть различными. Поэтому, числа больше 990 нам не подходят.
Значит, число сотен искомого числа равно 9, число десятков равно 8. Ищем число единиц.
Чтобы число делилось на 6, надо, чтобы оно делилось на 2 (т.е. было чётным) и делилось на 3 одновременно. Чтобы число делилось на 3, сумма его цифр должна делиться на 3.
984 - подходит под все условия задачи.
984 - четное, т.к. оканчивается на чётную цифру (4) и сумма цифр числа делится на 3 (9+8+4=21, 21:3=7).
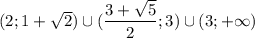
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть 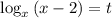 . Тогда
. Тогда 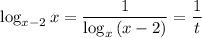 :
:
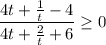 . Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма
. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 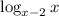 равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
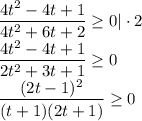
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
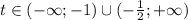
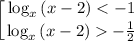
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
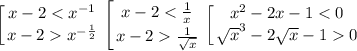
Первое неравенство имеет решение (с учётом ОДЗ) 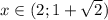
Второе неравенство раскладывается на множители:
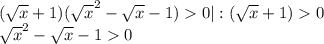
Нули получившегося неравенства: 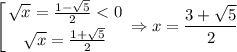
C учётом ОДЗ получаем, что в данном случае 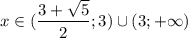 (левая граница меньше правой, так как √5 < 3).
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
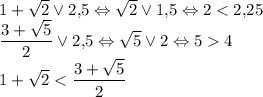
Тогда промежутки не пересекаются, итоговый ответ: