ответ: p=178/297.
Пошаговое объяснение:
Событие А - студенту досталась задача повышенной сложности - может произойти вместе с одним из событий A1 и A2, называемых гипотезами:
A1 - преподаватель переложил из второго конверта в третий простую задачу:
А2 - задачу повышенной сложности.
Тогда по формуле полной вероятности P(A)=P(A1)*P(A/A1)+P(A2)*P(A/A2).
Но P(A/A1)=6/11, а P(A/A2)=7/11. Остаётся найти P(A1) и P(A2). Заметим сразу, что так как события A1 и A2 несовместны и притом образуют полную группу, то P(A1)+P(A2)=1, откуда P(A2)=1-P(A1). Событие A1 может произойти совместно с одной из 4-х гипотез:
H1 - преподаватель переложил из первого конверта во второй две простых задачи;
H2 - две задачи повышенной сложности;
H3 - простую и повышенной сложности;
H4 - повышенной сложности и простую.
Тогда по формуле полной вероятности P(A1)=P(H1)*P(A1/H1)+P(H2)*P(A1/H2)+P(H3)*P(A1/H3)+P(H4)*P(A1/H4). Но P(H1)=8/12*7/11=56/132=14/33; P(H2)=4/12*3/11=12/132=3/33; P(H3)=8/12*4/11=32/132=8/33; P(H4)=4/12*8/11=32/132=8/33; P(A1/H1)=8/18; P(A1/H2)=6/18; P(A/H3)=P(A/H4)=7/18.
Отсюда P(A1)=121/297 ⇒P(A2)=1-121/297=176/297 и тогда P(A)=121/297*6/11+176/297*7/11=178/297.
16π+4√2 см²
Пошаговое объяснение:
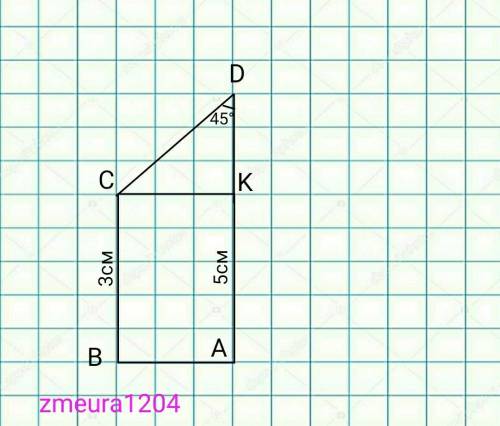
CB=AK=3см
КD=AD-AK=5-3=2см
∆СKD- прямоугольный равнобедренный треугольник
(<СКD=90°; <CDK=45°; <DCK=45°) углы при основании равны. СК=KD=2см
По теореме Пифагора
СD=√(CK²+KD²)=√(2²+2²)=2√2 см
СК=ВА=2см.
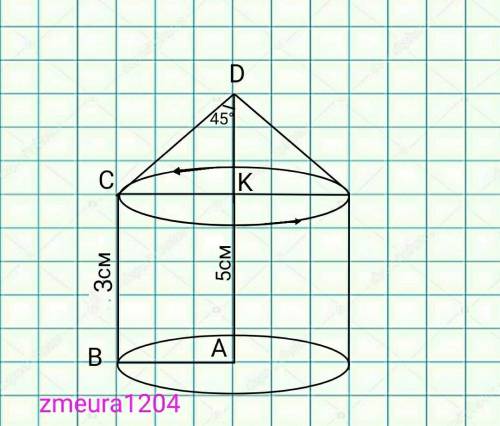
При вращении получили конус и цилиндр с равным радиусом
R=CK=BA=2см
Sбок.к.=πRL=π*CK*CD=π*2*2√2=4√2π см² площадь боковой поверхности конуса
Sбок.ц=2πRh=2π*BA*BC=2π*2*3=12π см² площадь боковой поверхности цилиндра.
Sосн.ц=πR²=π*2²=4π см² площадь основания цилиндра.
Sз.ф.=Sбок.к+Sбок.ц+Sосн.ц=
=4√2π+12π+4π=16π+4√2π см² площадь заданной фигуры.