1/log(x-1)x/6 >= -1
logf(x) g(x) или logf(x) h(x) (f(x)-1)(g(x) - h(x)) или 0
log(a)b a>0 b>0 a≠1
знаменатель не равен 0
ОДЗ x-1> 0 x>1
x-1≠1 x≠2
x/6>0 x>0
x/6 ≠ 1 x≠6
x∈(1 2) U (2 6) U (6 +∞)
log(x-1) x/6 = a
1/a >= -1
(1 + a) / a >=0
[-1] (0)
a∈(-∞ -1] U ( 0 +∞)
1. log(x-1) x/6 <= -1
log(x-1) x/6 <= log(x-1) (1/(x-1))
(x-2)(x/6 - 1/(x-1)) <=0
(x-2)(x² - x - 6)/(x-1) <=0
D=1+24=25 x12=(1 +-5)/2 = 3 -2
(x-2)(x-3)(x+2)/(x-1) <=0
[-2] (1) [2] [3]
x∈[-2 1) U [2 3]
2/ log(x-1) x/6 > 0
log(x-1) x/6 > log(x-1) 1
(x-2)(x/6 - 1) >0
(x-2)(x-6) > 0
(2) (6)
x∈(-∞ 2) U (6 +∞)
ответы 1 и 2 пересекаем с ОДЗ x∈(1 2) U (2 6) U (6 +∞)
ответ х∈(2 3] U (6 +∞)
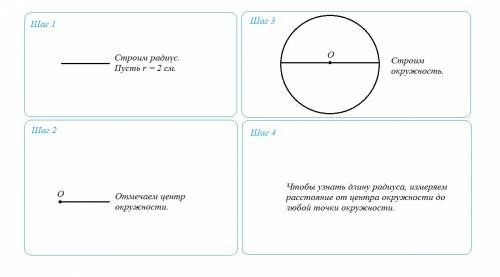
1) Строим отрезок, равный радиусу. Например, 2 см. То есть r = 2 см.
2) Отмечаем центр окружности (им будет край отрезка).
3) Измеряем циркулем отрезок, проводим окружность. Раствор циркуля должен оставаться неизменным.
4) Прикладываем линейку к радиусу и "продлеваем" его до пересечения с окружностью.
5) Чтобы узнать длину радиуса, нужно измерить расстояние от центра окружности до любой точки окружности.
упрощённый)
1) Берем произвольную длину радиуса. Пусть r = 2 см.
2) Так как радиус равен половине диаметра, то получаем следующее (вместо r подставляем значение радиуса):
d = 2r ⇒
d = 2·2 = 4 (см) - длина диаметра.
3) Отмечаем центр отрезка (диаметра). Это будет центр окружности.
Пусть O – центр окружности.
4) Строим окружность с центром в точке О.
5) Чтобы узнать длину радиуса, измеряем расстояние от центра окружности до любой точки окружности.