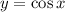
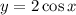
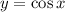 . Отличается лишь область значений.
. Отличается лишь область значений.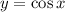 область значений следующая:
область значений следующая:![E(\cos x)=[-1,1]](/tpl/images/0579/2389/1dd9b.png)

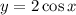 :
: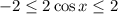
![E(y)=[-2,2]](/tpl/images/0579/2389/4690c.png)
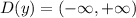 - область определения
- область определения 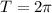 - период функции (все тригонометрические функции периодичны) .
- период функции (все тригонометрические функции периодичны) .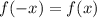
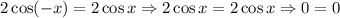 - тождество.
- тождество.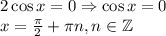
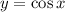 достигает экстремумы на концах отрезка области значения, то и
достигает экстремумы на концах отрезка области значения, то и 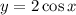 достигает экстремумы на концах отрезка:
достигает экстремумы на концах отрезка:![[-2,2]](/tpl/images/0579/2389/82b6c.png)
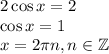 - максимумы.
- максимумы.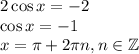 - минимумы.
- минимумы. и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на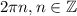
 и на интервалах, получаемые сдвигом этого интервала на
и на интервалах, получаемые сдвигом этого интервала на 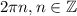
![[\pi,2\pi]](/tpl/images/0579/2389/a222e.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 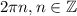
![[0,\pi]](/tpl/images/0579/2389/2a07b.png) и на отрезках, получаемых сдвигами этого отрезка на
и на отрезках, получаемых сдвигами этого отрезка на 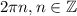

Общая схема исследования и построения графика функции
у=-х³-5х+3
1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.
Вся числовая ось, разрывов нет.
2. Выяснить, является ли функция четной или нечетной. Ни та, ни другая.
3. Выяснить, является ли функция периодической. Нет.
4. Найти точки пересечения графика с осями координат (нули функции).
у = 0, х = 0,56410,
х = 0, у = 3.
5. Найти асимптоты графика. Нет.
6. Вычислить производную функции f'(x) и определить критические точки.
Производная равна -3х² - 5.
7. Найти промежутки монотонности функции. Функция убывающая на всё числовом промежутке.
8. Определить экстремумы функции f(x). Производная не может быть равна нулю(х² отрицателен), экстремумов нет.
9. Вычислить вторую производную f''(x) = -6x. x = 0.
10. Определить направление выпуклости графика и точки перегиба.
Вогнутая на промежутках (-oo, 0].
Выпуклая на промежутках [0, oo).
Перегиб в точке х = 0.
11. Построить график, используя полученные результаты исследования.
Дан в приложении.