Постараемся найти (как требует условие) методом подбора хотя бы одно целое решение системы.
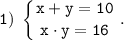
Так как произведение целых чисел х и у равно положительному числу 16, то
а) числа х и у одного знака;
б) х и у являются делителями числа 16.
Но x + y = 10, исходя из этого в силу свойства а) заключаем, что числа х и у положительные.
Далее, положительными делителями числа 16 будут целые числа:
1, 2, 4, 8, 16.
Из этих чисел можно составить только пары (2; 8) и (8; 2), которые удовлетворяют условию x + y = 10.
ответ: (2; 8), (8; 2).
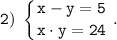
Так как произведение целых чисел х и у равно положительному числу 24, то
а) числа х и у одного знака;
б) х и у являются делителями числа 24.
Но x - y = 5, исходя из этого в силу свойства а) заключаем, что x > y.
Далее, положительными делителями числа 24 будут целые числа:
1, 2, 3, 4, 6, 8, 12, 24.
Из этих чисел можно составить только пару (8; 3) (x>y выполняется), которая удовлетворяет условию x - y = 5. Но, если x и y отрицательные, то пара (-3; -8) также (x>y выполняется) удовлетворяет условию x - y = 5.
ответ: (8; 3), (-3; -8).
S=3,14*(1.4)²=3,14*1,96≈6,2