- √(2а-2).
Пошаговое объяснение:
(1-а)√(2/(а-1))
1. По определению арифметического квадратного корня подкоренное выражение 2/(а-1)≥0. Так как 2>0, то и а-1>0.
2. Разность а-1>0, тогда противоположная ей разность 1-а < 0.
Вносить под знак арифметического квадратного корня можно лишь неотрицательные множители.
Преобразуем выражение так:
(1-а)√(2/(а-1)) = -1•(а-1)√(2/(а-1)) .
Теперь множитель (а-1) неотрицательный, вносим его под знак корня, возведя в квадрат. Другой множитель -1 так и останется перед корнем.
Полное решение можно записать так:
(1-а)√(2/(а-1)) = -1•(а-1)√(2/(а-1)) = -√(2(а-1)^2/(а-1)) = - √(2(а-1)) = - √(2а-2).
Если убрать две первые цифры, то получится двузначное число, которое, согласно условию, является четвертой степенью целого числа. Среди двузначных чисел таких всего два: 16=2⁴ и 81=3⁴;
Если убрать первую цифру слева, то получим трехзначное число - куб по условию. Кубов среди трехзначных чисел немного, вот они: 5³, 6³, 7³, 8³ и 9³. При этом последние две цифры должны быть 16 или 81 (см. выше).
Таким образом, подходит только 6³. Остается найти число x такое, что x216 - квадрат. Можно записать: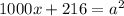 
; Взяв это равенство по модулю 3, получим: 
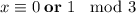(так как квадрат числа дает остаток или 1, или 0 при делении на 3).
Значит, x равен 1, 3, 4, 6, 7 или 9. (можно было объяснить проще: x+2+1+6 - сумма цифр искомого числа дает тот же остаток от деления на 3, что и само число [известное свойство], откуда и вытекает полученное). Можно перебрать оставшиеся числа, а можно предположить, что число делится на три. Тогда остаются числа 3, 6, 9. Более того, искомое число делится и на 4. Значит, число делится на 12. Осталось проверить квадраты чисел 36, 48, 60, 72, 84, 96. Но искомое число оканчивается на 6, поэтому к рассмотрению подлежат лишь 36 и 96. Легкой проверкой убеждаемся, что 96 подходит. Искомое число - 9216
х-у=2
а-х=3
Сложим эти два уравнения: х-у+а-х=5
а-у=5
Значит, утка легче щенка на 5 кг.