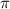в математике, по определению, равно отношению длинны 
произвольной окружности к диаметру 
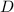той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
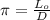формула [1] ;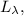
составляющую 
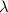часть от длины всей окружности, в данном конкретном случае 
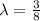от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть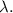 
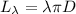формула [2] ;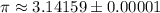
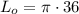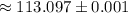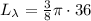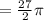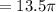см 
см ;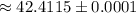
см 
см 
см 
см ;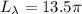
см ;
см .
Боковая сторона равносторонняя трапеции 10√2 см. Она образует с основанием куд 45 градусов. Найти площадь трапеции, если в нее можно вписать окружность.
Пошаговое объяснение:
Прочитаем задачи:
Боковая сторона равнобедренной трапеции равна десять корней из двух, и образует с основанием угол 45 градусов.Найти площадь трапеции если в нее можно вписать окружность.
Опустим ВК⊥АD, ∠А = ∠АВК = 45 ° ⇒ВК = АК
АВ² = 2ВК²⇒ВК = √АВ² / 2 = 10.
В четырехугольник можно вписать окружность тогда, когда суммы противоположных сторон четырехугольника равни.⇒
АВ + CD = BC + AD = 2 * 10√2 = 20√2
S = BK * (BC + AD) / 2 = 10 * (20√2) / 2 = 100√2.