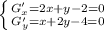
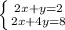
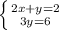
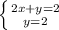
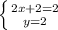
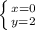
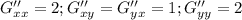
![H= \left[\begin{array}{cc}2&1\\1&2\end{array}\right]](/tpl/images/0853/6384/c158e.png)
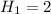 - 1 минор положительный.
- 1 минор положительный.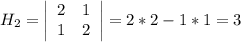 - 2 минор положительный.
- 2 минор положительный.х = -20; у = -2
Пошаговое объяснение:
Решим данную систему уравнений методом сложения. Но для этого умножим левую и правую части первого уравнения на 2:
(8у - х)*2 = 4*2
16у - 2х = 8
Теперь прибавим левые части уравнений и приравняем их к сумме правых частей:
16у - 2х + 2х - 21у = 8 + 2
2х - 2х + 16у - 21у = 10
0х - 5у = 10
-5у = 10
Разделим левую и правую части уравнения на (-5):
у = -10/5
у = -2
Подставим получившееся значение у в исходное первое уравнение системы:
8у - х = 4
8 * (-2) - х = 4
-16 - х = 4
х = -20
Имеем ответ: х = -20; у = -2
Вот так как-то)