а)
2x+5≤12
-x+4<-5x
2x≤7
4x<-4
x≤3.5
x<-1
ответ: х є (-∞;-1).
b)
4x>2
x-3<2x+1
x>0.5
-x<4
x>-4
x>0.5
ответ: х є (0.5;+∞).
с)
3х+1<5х-7
8х-6<7х
-2х<-8
х<6
х>4
х<6
ответ: х є (4;6)
В неравенствах, как и в уравнениях, слагаемые можно переносить через знак <,≤,>,≥ изменяя при этом знак на противоположный.
Домножать или делить неравенства на какое то число можно, если вы знаете его знак.
Если число положительное, ничего не изменится.
Если число отрицательное, знак <(≤) изменяется на >(≥), знак >(≥) изменится на <(≤).
Если будут вопросы – обращайтесь :)
Длина окружности вычисляется по формуле
C = 2·π·R
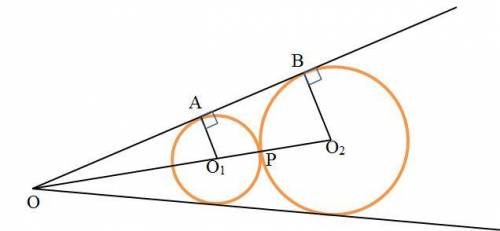
Дано (см. рисунок)
С(2) = 12 см - длина окружности с центром в точке О₂
ОО₂=30 см
Найти: С(1) - длина окружности с центром в точке О₁
Решение.
Из С(2) = 12 см находим радиус большой окружности
2·π·R₂ = 12 см или R₂ = ВО₂ =6/π см .
Длина меньшей окружности равна С(1)=2·π·АО₁ .
Радиусы обоих окружностей перпендикулярны к прямой ОВ, то есть углы О₁АО=О₂ВО. С другой стороны угол АОО₁= ВОО₂ и поэтому верно первый признак подобия треугольников:
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны..
Тогда по свойству подобных треугольников получим:
ВО₂ : ОО₂=АО₁ : ОО₁
Но ОО₁=ОО₂-О₂Р-РО₁ или ОО₁=ОО₂-ВО₂-АО₁. Тогда
ВО₂ : ОО₂=АО₁ : (ОО₂-ВО₂-АО₁)
Отсюда
ВО₂·(ОО₂-ВО₂) - ВО₂·АО₁ = АО₁ · ОО₂
(ОО₂ + ВО₂)·АО₁ = ВО₂·(ОО₂-ВО₂)
АО₁ = ВО₂·(ОО₂-ВО₂) : (ОО₂ + ВО₂) = 6/π· (30-6/π) : (30 + 6/π)
Теперь вычислим длину меньшей окружности
С(1)=2·π·АО₁ = 2·π·6/π·(30-6/π) : (30 + 6/π)=
=12·(30-6/π) : (30 + 6/π)=12·(30·π-6) : (30·π + 6).
ответ: 12·(30·π - 6)/(30·π + 6)
сначала 4х, потом 4х-128, потом (4х-128)*13 и получили 52
(4х-128)*13 =52
52х-1664=52
52х=52+1664
52х=1716
х=1716/52
х=33
ответ:33