В прямоугольном параллелепипеде все грани - прямоугольники, все рёбра равны и перпендикулярны основаниям.
Формула диагонали квадрата d=a√2 ⇒
Диагональ АС основания равна 4√2
Из прямоугольного треугольника АА1С по т.Пифагора боковое ребро
АА1=√(А1С²-AC²)=√(81-32)=7 (ед. длины)
-------
Вариант решения.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Измерениями прямоугольного параллелепипеда являются длины трех ребер, исходящих из одной его вершины. Отсюда следует:
D²=a²+b²+c², где а и b- стороны основания, с - боковое ребро.
По условию а=b=4. D=9
81=16+16+c² ⇒
c²=81-32=49
c=7 - длина бокового ребра.

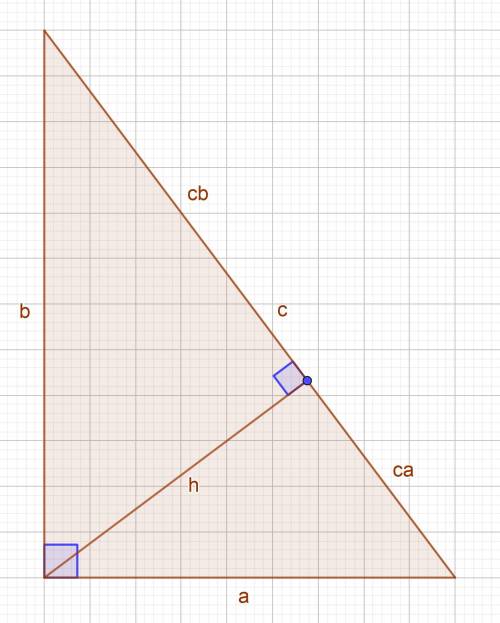
Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.
Исходя из т. Пифагора, следует:
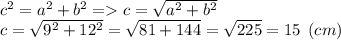
Найдет площадь прямоугольного треугольника:

Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:
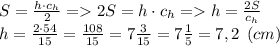
Проекции катетов будут равны:
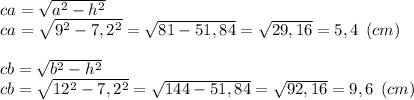
или 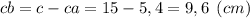
—————————————————————————————
Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:
– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:
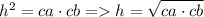
– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
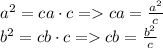
—————————————————————————————
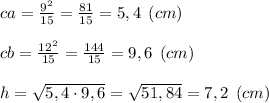
ответ: гипотенуза равна 15 см, высота — 7,2 см, проекции катетов — 5,4 см и 9,6 см.