ответ:
основу любой электрической схемы представляют условные графические обозначения различных элементов и устройств, а также связей между ними. язык современных схем подчеркивает в символах подчеркивает основные функции, которые выполняет в схеме изображенных элемент. все правильные условные графические обозначения элементов электрических схем и их отдельных частей приводятся в виде таблиц в стандартах.условные графические обозначения образуются из простых фигур: квадратов, прямоугольников, окружностей, а также из сплошных и штриховых линий и точек. их сочетание по специальной системе, которая предусмотрена стандартом, дает возможность легко изобразить все, что требуется: различные электрические аппараты, приборы, электрические машины, линии механической и электрической связей, виды соединений обмоток, род тока, характер и способы регулирования и т. п.
кроме этого в условных графических обозначениях на электрических принципиальных схемах дополнительно используются специальные знаки, поясняющие особенности работы того или иного элемента схемы.
пошаговое объяснение:
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от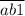 
до 
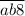, либо от 
до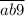 
.
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
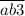, делящееся на 3
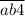, делящееся на 4
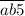, делящееся на 5
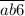, делящееся на 6
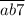, делящееся на 7
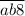, делящееся на 8
Рассмотрим утверждение "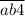 делится на 4". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 
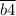делится на 4, 
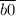делится на 4, 
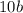делится на 4, 
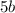делится на 2, значит 
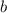- четное.
Рассмотрим утверждение "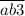 делится на 3". Число делится на 3, если сумма цифр числа делится на 3. Значит, 
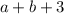делится на 3, 
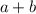делится на 3. Выпишем пары цифр, где 
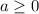, а 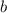- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение "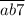 делится на 7". Если 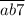делится на 7, то 
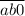делится на 7, 
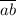делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13
нок (225, 45, 270)=1350