Математика: 8+12÷4×3 20-10÷(2+8) (16+4)÷5×4 (6+3)×5-40÷5 100-(81+9÷8) (20-10)÷2+8 12+18÷3-5 6+3×5-40÷5

8+12÷4×3 20-10÷(2+8) (16+4)÷5×4 (6+3)×5-40÷5 100-(81+9÷8) (20-10)÷2+8 12+18÷3-5 6+3×5-40÷5

👇

Увидеть ответ

Ответ:

dayana20072

19.05.2021

1 )17
2)19
3)16
4)37
5)17,875
6)13
7)13
8)13

4,4(29 оценок)

Ответ:

marisina

19.05.2021

1) 17
2) 19
3)16
4)37
5) 17.875
6) 13
7) 13
8) 13

4,8(51 оценок)

Открыть все ответы

Ответ:

Botan0011

19.05.2021

Из знаменателя нам нужно только взять ограничение подкоренного выражения, которое и будет являться областью определения неравенства (в числителе ограничений нет): $x+4\geq 0 \Rightarrow \boxed{x\geq -4}$

Помним про это.

Теперь решаем само неравенство

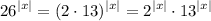$\displaystyle 26^{|x|}=(2\cdot 13)^{|x|}=2^{|x|}\cdot 13^{|x|}$ - это нам потребуется

Заметим, что 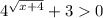$\displatstyle 4^{\sqrt{x+4}}+3 0$ для любых , поэтому умножим все неравенство на знаменатель и ничего не поменяется, избавимся от дроби. И сразу запишем в числителе то, что уже преобразовали.

$\displaystyle 2^{|x|}\cdot 13^{|x|}-2^{|x|}-2\cdot 13^{|x|}+2\geq 0 ;\ 13^{|x|}(2^{|x|}-2)-(2^{|x|}-2)\geq 0; \\ (2^{|x|}-2)(13^{|x|}-1)\geq 0$

Чтобы решить полученное неравенство методом интервалов, найдем нули выражения, стоящего левее знака:

$\displaystyle \\ (2^{|x|}-2)(13^{|x|}-1)= 0 \Leftrightarrow \left [ {{2^{|x|}-2=0} \atop {13^{|x|}-1=0} \right. \Rightarrow \left [ {{2^{|x|}=2^1} \atop {13^{|x|}}=13^0} \right. \Rightarrow \\ \left [ {{|x|=1} \atop {|x|=0}} \right. \Rightarrow \left [ {{x=\pm1} \atop {x=0}} \right.$

Замечательно, теперь ничего не мешает использовать метод интервалов. Заметим, что функция, у которой мы нули находили - четная, так как везде с иксами модули стоят, поэтому 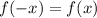f(-x)=f(x) , и нули тоже симметричны. То есть можно найти знаки на положительных значениях, а на отрицательных симметрично относительно нуля расставить.

На $(1;+\infty)$ обе скобки при подстановке какого-либо числа положительны, все выражение положительно (+).

На (0;1) (можно взять как пример 0.5, так как это степень, это будет корень второй степени, то есть обычный корень) вот что получается:

$(\sqrt{2}-2)(\sqrt{13}-1)$ , первая скобка отрицательна, вторая положительна, то есть выражение отрицательно (-).

Теперь симметрично отображаем и получаем на 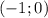(-1;0) отрицательно (-)

А на 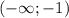$(-\infty; -1)$ положительно (+).

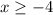
То есть надо было бы взять $x\in(-\infty;-1]\cup \{0\} \cup [1;+\infty)$ , не забываем брать сами нули, так как неравенство нестрогое, но вспомним про ограничение из знаменателя, которое $x\geq -4$

Накладывая ограничение, получим итоговый ответ:

$\boxed{x\in[-4;-1]\cup \{0\}\cup[1;+\infty)}$

То есть это самый последний, 5-ый ответ из тех, что можно выбрать.

4,4(8 оценок)

Ответ:

253n

19.05.2021

S = a•c
S = b•d
Отсюда для вычисления в таблице:
a•c = b•d

В таблице столбик а):
а = 4 см
b = 2 см
c = 1 см
d = 2 см (так как a•c = b•d, значит, d = a•c/b)
S = 4 кв.см (так как S = a•c или S = b•d)

В таблице столбик б):
а = 6 дм (так как a•c = b•d, значит, а = b•d/c)
b = 1 дм
c = 0,5 дм
d = 3 дм
S = 3 кв.дм (так как S = a•c или S = b•d)

В таблице столбик в):
а = 30 м (так как S = a•c, значит, а = S:с)
b = 4 м (так как S = b•d, значит, b = S:d)
c = 2 м
d = 15м
S = 60 кв.м

В таблице столбик г):
а = 15 см
b = 1 дм
c = 50/15 = 10/3 = 3 1/3 см (так как S = a•c, значит, с = S:а)
d =50/10 = 5 см (1 дм = 10 см и так как S = b•d, значит, d = S:b)
S = 50 кв.см

4,6(92 оценок)

Это интересно:

Компьютеры-и-электроника

01.08.2022

Как сохранить фото на Macbook: простые способы...

Питомцы-и-животные

09.08.2021

Как приготовить угощения для лошади: рецепты и советы...

Компьютеры-и-электроника

19.02.2022

Как отправить личное сообщение в Instagram...

Образование-и-коммуникации