2) KL² =NL*LM² NL =x LM=MN -NL =25 -x;
144 =x(25 -x) ;
x² -25x +144 =0;
x = 9
x=16 (по рисунку NL < LM )
ΔKLN : NK² =NL²+ LK²
NK =3*5 =15 (9 =3*3; 12=3*4; 3*5=15)..
ΔKLM : KM² =KL² +LM²
KM =4*5 =20 (12 =4*3; 16=4*4 ;4*5 =20)
3) KE² =EM*EL
EM =KE²/EL =6²/8 =9/2 =4,5
KL² =KE² +EL² =6² +8² =100 =10²
KL =10.
KL² =ML*EL
ML =KL²/EL =100/8 =12,5.;
( 5/EM = ML --EL =12,5 -8 =4,5)
MK² =ML*ME;
MK² =12,5*4,5 =25*0,5*0,5*9;
MK =5*0,5*3 =7,5.
4) MN² =MK² +KN² =5² +²12² =25 +144 =169 =13²;
MN =13;
MK² =MN*MT ;
MT =MK²/MN=5²/13 =25/13.
NT =MN -MT =13 -25/13 =144/13;
KT² =MT*NT=25/13*144/13 =(5*12/13)² ;
KT =5*12/13 =60/13.
или из ΔMTK :
KT² =MK² -MT²² =5² -(25/13)² =(5 -25/13)(5+25/13) =40/13*90/13 =(2*3*10/13)²;
KT =2*3*10/13 =60/13 .
Пошаговое объяснение:
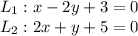
найдем точку пересечения прямых. для этого решим систему уравнений
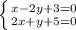
из первого выразим х х= 2у-3
подставим во второе 2(2у-3)+у+5=0; 4у -6 +у +5 =0; 5у=1; у=0,2
тогда х = 2*0,2 -3 = 0,4 -3 = -2,6
это наша точка пересечения М(-2,6; 0,2)
теперь уравнение прямой, параллельной оси оу
направляющий вектор оси оу s=(0;1), можем его использовать в качестве направляющего вектора искомой прямой, т.к. они параллельны
тогда каконическое уравнение прямой, проходяшей через точку М(-2,6; 0,2) параллельно оси оу будет
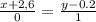
перейдем к обшему виду и получим
х = -2,6