Пошаговое объяснение:
Дано:
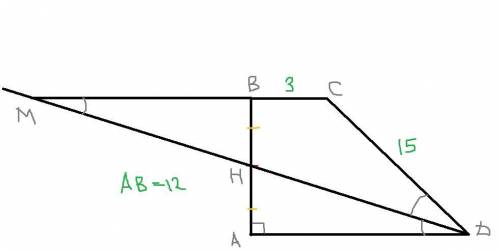
BC=3
AB=12
CD=15
AH=HB
∠ADH=HDC
Найти:
AD - большее основание трапеции АВСD
BA - высота трапеции АВСD
В трапеции АВСD биссектрису HD продолжим до точки M . При этом продолжим меньшее основание ВС у трапеции ABCD,также до точки M пересечения с продолжением биссектрисы HD. Исходя из сделанного дополнительного построения получаем,что углы ∠ADH=∠HDC=∠CMD . Так как ∠ADH=∠HDC=∠CMD,то треугольник MCD является равнобедренным,то есть MC=CD и поэтому сторона MC=15.
Если нам известно,что MC=15,а малое основание ВС=3,то MB=12.
Так как нам известно из условия,что AH=HB ,то опираясь на признаках равенства треугольников получаем,что ΔMBH=ΔHAD,следовательно MB=AD=12.
Высота в это случае равна AB,то есть AB=h=12
ответ: Большее основание трапеции ABCD - AD=12
Высота трапеции ABCD равна 12
1) a-b=-3 - разность отрицательная. значит a<b
a=-3+b
a=b-3
a < b
2) a - b = 2/7 - разность положительная. значит a>b
a=2/7+b
a=b+2/7
a > b
3) a - b=0 - разность = 0. значит a=b
a=0+b
a=b
4) a - b= -0.5 - разность отрицательная, значит a<b
a=-0.5+b
a=b-0.5
a < b
5) b-a=1 - разность положительная, значит b>a
b=1+a
b=a+1
b > a
6) b - a=-0.99 - разность отрицательная. значит b<a
b=-0.99+a
b=a-0.99
b < a
б)0,357кг; 0,0205кг(не уверена) 5100кг, 1,125кг