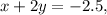
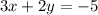
сложения. Нам нужно сделать так, чтобы при сложении какая-то из переменных исчезла. Модуль переменной дожен быть равен в двух уравнениях, а знаки разные. Нужно выбрать любую из переменных. Тут проще взять 2y. Необходимо, чтобы в одном уравнении было 2y, а в другом — -2y. Для этого домножим одно из уравнений на -1.
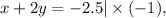
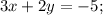
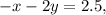
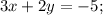
Теперь можно сложить.
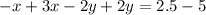
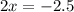
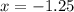
Одна из переменной известна. Нужно подставить это значение в любое из уравнений системы.
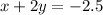
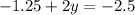
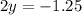
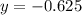
ответ: –1.25; –0.625
подстановки. Метод заключается в том, что нужно выразить переменную из одного уравнения и подставить другое. Тут, опять же, проще начать с первого уравнения. Выразим x.
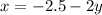
Теперь подставляем во второе уравнение.
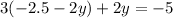
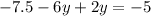
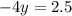
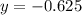
Полученное значение y подставляем в первое выражение.
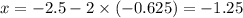
ответ: –1.25; – 0.625
A=0,(2021); 10000A=2021,(2021)=2021+A; 9999A=2021; A=2021/9999;
3,(2021)=3+A=3+2021/9999=32018/9999; m=32018; n=9999.
Докажем, что m и n взаимно просты.
Для этого достаточно доказать взаимную простоту чисел 2021 и 9999. Применять алгоритм Евклида лень, проще разложить 9999 на простые множители.
9999=3·3·1111=3·3·11·101. Кто сомневается в простоте числа 101, попробуйте поделить его на 2, 3, 5 и 7 (следующий простой потенциальный делитель - это 11, что больше корня из 101; если бы был такой делитель, то был был и делитель 101/11, меньший корня из 101).
У числа 2021 нет делителей 3, 11 или 101, поэтому взаимная простота доказана.
ответ: m=32018; n=9999