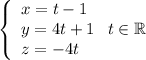ответ:Пусть местное время в Сиднее отличается на от местного времени в Лос-
Анджелесе. Самолёт взлетел в 22:40 в среду, а приземлился в 8:40 в пятницу. Без учёта сдвига
часовых поясов, разница составляет 34 часа, поэтому время полёта равно 1 = 34 ч − . При
полёте в обратном направлении время, как кажется, идёт назад (на 5,5 часов). Следовательно,
обратный перелёт длился 2 = − 5,5 ч.
Скорость самолёта в первом случае была на 10% меньше, поэтому время в пути из Лос-
Анджелеса в Сидней было в 10/9 раз больше, чем во втором случае:
= 10 2
⇒ 34 ч − = 101
9 ( − 5,5 ч) ⇒ = 19 ч.
1.
Уравнение плоскости, проходящей через некоторую точку с координатами (x₀,y₀,z₀), в общем виде записывается так:
A(x-x₀) + B(y-y₀) + C(z-z₀)= 0, где коэффициенты A,B,C - координаты вектора нормали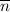 
Найдём вектор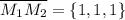 
Вектор нормали 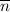найдём из векторного произведения векторов a и M₁M₂
![\overline{n} =[\overline{a}~\times~\overline{M_1M_2}] = \begin{vmatrix} \overline i & \overline j & \overline k \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{vmatrix} = \overline i - \overline k = \{1, 0, -1\}](/tpl/images/0215/8850/4d6c7.png)
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему: 
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Пусть z = -4
Снова решим систему: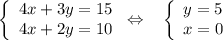 
Координаты точки B(0, 5, -4)
Найдём направляющий вектор прямой
Запишем уравнение прямой в каноническом виде: 
И в параметрическом виде: 
