Сторону квадрата увеличили на 15%. на сколько процентов увеличилась его площадь?

Question

Математика: Сторону квадрата увеличили на 15%. на сколько процентов увеличилась его площадь?

Strelok09245 · Accepted Answer

Произведение всех делителей числа, не являющегося точным квадратом есть некоторый точный квадрат.

Так как у числа n 6 делителей, то есть четное число делителей, то оно не является точным квадратом.

Разложим число 432 на простые множители:

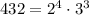
$432=2^4\cdot3^3$

Таким образом, необходимо, чтобы шестой делитель имел в своем разложении на простые множители сомножитель 3 в нечетной степени.

Из предложенных чисел только число 12 удовлетворяет этому условию.

Действительно, в это случае произведение всех делителей будет являться точным квадратом:

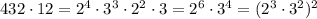
$432\cdot12=2^4\cdot3^3\cdot2^2\cdot3=2^6\cdot3^4=(2^3\cdot3^2)^2$

ответ: 12