h=13,5
Пошаговое объяснение:
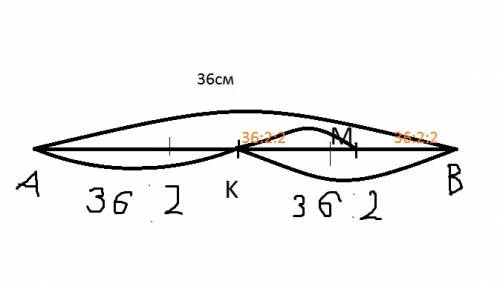
Р=4*ВС
ВС=Р/4=90/4=22,5 сторона ромба
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.
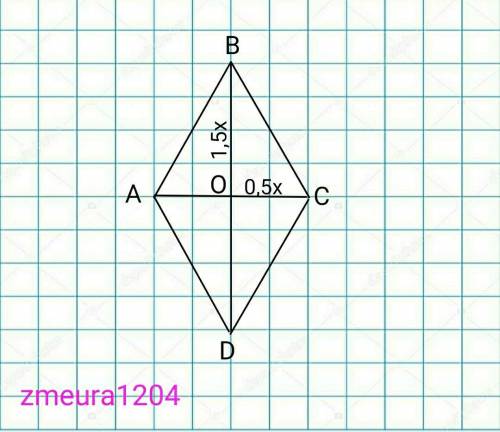
Пусть диагональ ромба АС будет х, а ВD 3х.
Тогда ОС=АС/2=х/2=0,5х; ВО=ВD/2=3x/2=1,5x.
∆ВОС- прямоугольный треугольник
По теореме Пифагора
ВО²+ОС²=ВС²
Составляем уравнение
(0,5х)²+(1,5х)²=22,5²
0,25х²+2,25х²=506,25
2,5х²=506,25
х²=506,25/2,5
х²=202,5
х=√202,5
АС=√202,5
ВD=3*√202,5
S=1/2*AC*BD=1/2*3√202,5*√202,5=
=1/2*3*202,5=303,75
S=h*a, где а- сторона ромба; а=22,5
h=S/a=303,75/22,5=13,5
Відповідь:
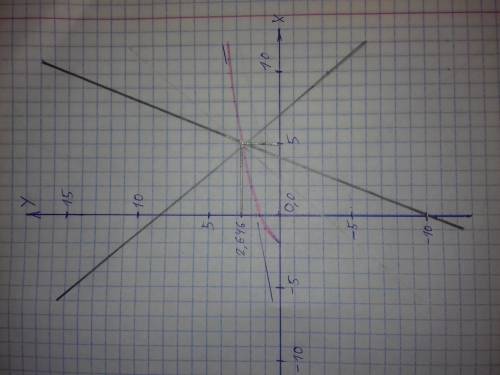
Угловой коэффициент прямой ( больший по модулю ) к = 2,856
Покрокове пояснення:
Задана функция у = sqrt ( x + 2 )
При х = 2, у = sqrt ( 5 + 2 ) = 2,646
Определим угол наклона функции в точке с координатами ( 5; 2,646 ). Вычислим значения функции в точках находящихся слева и справа на небольшом удалении это точки ( 4,99; 2,644 ) и ( 5,01; 2,648 ). При смещении х на величину 0,02, у изменяется на 0,00378.
0,00378 / 0,02 = 0,189 - это соответствует углу 10,702°.
По условиям задачи искомая прямая должна проходить через точку с координатами ( 5; 2,646 ) под углом 60° к графику функции у = sqrt ( x + 2 ), это возможно при наклоне прямой под углами
1) 10,702° + 60° = 70,702°
2) 10,702° - 60° = -49,298°
Уравнение прямой у = кх + в. Определим коэффициент наклона прямой.
1) к = tg ( 70,702 ) = 2,856
2) к = tg ( -49,298 ) = -1,163
Определим в подставив координаты точки ( 5; 2,646 ) в уравнение.
1) 2,646 = 2,856 × 5 + в
в = -11,633
Искомое уравнение имеет вид
у = 2,856 × х - 11,633
2) 2,646 = -1,163 × 5 + в
в = 8,458
Искомое уравнение имеет вид
у = -1,163 × х + 8,458