8/125-50р-р^2-р^-1
8р-50р^2-125р^3+125/125р
-125р^3 - 50р^2+8р+125/125р
В решении.
Пошаговое объяснение:
у скільки разів найменше спільне кратне даних чисел більше за їх найбільший спільний дільник:20,35,75?
20=1*2*2*5
35=1*5*7
75=1*3*5*5
НОД=5;
НОК=2*2*5*7*3*5=2100;
2100 : 5 = 420.
ответ: НОК данных чисел больше НОД этих чисел в 420 раз.
Как найти:
НОД - это произведение общих множителей чисел, в данном случае это 1 и 5.
НОК определяется так:
а) разложить все числа на простые множители;
б) к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
в) к полученному произведению добавить недостающие множители третьего числа.
Итак, для ограничения по целым степеням не более 27 по модулю, вычислимыми оказались результаты ~957 млн выводов и среди них 356 являются выводами числа 5479 и ни один вывод (а соответственно ни один вывод с операциями сложения, вычитания, конкатенации, умножения и деления, а также некоторые выводы с этими же операциями и некоторыми целыми степенями) не является выводом числа 10958. В чем его особенность?
Призраки и тени
Для задачи, аналогичной задаче Танежи в восходящем порядке, но с начальными векторами длины 8, такими как $(1, 2, ... , 8)$ и $(2, 3, ... , 9)$ количество вариантов меньше, а с иррациональными, комплексными и длинными целыми значениями элементов векторов (1) — (7) справляются оптимизированные алгоритмы Вольфрам Математики. Так, достоверно известно, что ни один вывод в $(1, 2, ... , 9)$, имеющий на 8-ой итерации оператор конкатенации, сложения или вычитания не может привести к значению 10958. Какие возможности для дальнейшего решения это даёт?
Число 10958 является полупростым. И если последняя итерация вывода не содержит сложение, вычитание и конкатенацию, то один из операндов на 8-ой итерации будет гарантировано включать 5479 в некоторой степени, за исключением двух случаев:
когда операнды кратны некоторым комплексно-сопряжённым
когда один из операндов содержит логарифм, основание или показатель которого кратны 5479
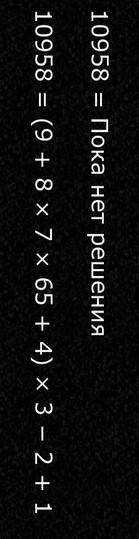
ответ: 0,064+p (-0,4-p+p^2)