АВК=40 градусов
Пошаговое объяснение:
Угол В=180-(А+С)=180-100=80 гардусов.Так как ВК биссектриса,то угол АВК=В:2=80:2=40 градусов
1.
Уравнение плоскости, проходящей через некоторую точку с координатами (x₀,y₀,z₀), в общем виде записывается так:
A(x-x₀) + B(y-y₀) + C(z-z₀)= 0, где коэффициенты A,B,C - координаты вектора нормали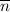 
Найдём вектор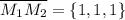 
Вектор нормали 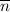найдём из векторного произведения векторов a и M₁M₂
![\overline{n} =[\overline{a}~\times~\overline{M_1M_2}] = \begin{vmatrix} \overline i & \overline j & \overline k \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{vmatrix} = \overline i - \overline k = \{1, 0, -1\}](/tpl/images/0215/8850/4d6c7.png)
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему: 
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Пусть z = -4
Снова решим систему: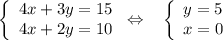 
Координаты точки B(0, 5, -4)
Найдём направляющий вектор прямой
Запишем уравнение прямой в каноническом виде: 
И в параметрическом виде: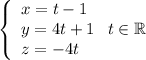 
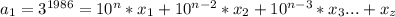
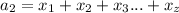заметим то что каждый член будет делится на 9 , потому сумма каждого числа делится на 9. То есть кратно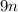 
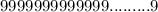то есть пусть она по количеству цифр будет равна количеству цифр числа 
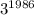, очевидно что это число будет иметь по крайней мере 
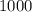цифр 
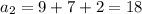
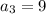, и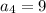 
, 
, 
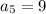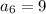, и.т.д и очевидно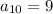 
Биссектриса треугольника - отрезок, выходящий из вершины угла треугольника и делящий его пополам.
По теореме о сумме углов треугольника:
∠A + ∠B + ∠C = 180°.
∠B = 180°- ∠A - ∠C = 180 - 70 - 30 = 80°.
∠ABK = 0,5∠B = 80 * 0,5 = 40°
ответ: 40°