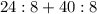
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
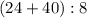
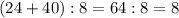В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на , то и их сумма делится на .
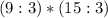
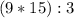
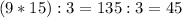
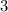,то их произведение делится на 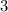" доказанным.
Пусть измерения параллелепипеда равны, например,
а = 2 см, b = 5 см и с = 4 см, тогда
V = abc = 2•5•4 = 40 (см^3),
S пов. = (2•5 + 2•4 + 5•4)•2 = (10+8+20)•2 = 38•2 = 76 (см^2).
Если речь идёт не просто об объёмном теле, а именно о кубе, то решение такое:
Пусть длина ребра куба а равна 2 дм. Все его измерения равны, тогда
V = a^3 = 2^3 = 8 (дм^3).
У куба шесть равных граней, каждая из которых является квадратом, тогда
S пов. = 6•а^2 = 6•2^2 = 6•4 = 24 (дм^2)