Имеется ряд шаров: красные, зеленые и желтые. желтых шаров 12, а количество зелёных шаров равно сумме желтых шаров и половины количества красных шаров. а количество красных шаров равно сумме зелёных и желтых шаров. сколько всего шаров имеется?

👇

Ответ:

МАМБЭТ

15.11.2020

Желтых 12 Зеленых 12+х/2 красных х и 24+х/2 следовательно Уравнение х=24+х/2 48+х=2х х=48 следовательно красных 36 Следовательно всего шаров 48+36+12=96

4,6(91 оценок)

Открыть все ответы

Ответ:

натуся103

15.11.2020

Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 3 с машинами и 7 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Миша. Найдите вероятность того, что Мише достанется пазл с машиной.

Эта задача на простейшую теорию вероятностей. Для ее решения воспользуемся следующей формулой:

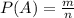$P(A)=\frac{m}{n}$ , где Р(А) - вероятность нашего события, m - количество благоприятствующих событий, а n - всевозможное количество событий.

В нашем случае нужны лишь события, в которых Мише достанутся пазлы с машиной, а их всего 3. Всего же событий - 10 (всего 10 комплектов). Подставим же значения в формулу и найдем вероятность:

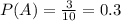
$P(A)=\frac{3}{10} =0.3$

ответ: 0,3

4,7(22 оценок)

Ответ:

yakurnovanasta

15.11.2020

На плоскости даны окружность ω , точка A, лежащая внутри ω , и точка B, отличная от A.
Рассматриваются всевозможные треугольники BXY, такие что точки X и Y лежат на ω и хорда XY проходит через точку A.
Докажите, что центры окружностей, описанных около треугольников BXY, лежат на одной прямой.

Решение:

По теореме о произведении отрезков хорд произведение XA • AY не зависит от положения хорды XY и равно некоторой постоянной величине d.
На продолжении отрезка BA за точку A отложим отрезок AC длины .
Тогда AB • AC = XA • AY = d, следовательно точки X, B, Y и C лежат на одной окружности.
Это означает, что окружности, описанные около треугольников BXY, проходят через фиксированные точки B и C,
следовательно их центры лежат на серединном перпендикуляре к отрезку BC.

Задача 2.В пространстве даны n точек общего положения
(никакие три не лежат на одной прямой, никакие четыре не лежат в одной плоскости, ).
Через каждые три из них проведена плоскость.
Докажите, что какие бы n – 3 точки в пространстве ни взять,
найдётся плоскость из проведённых, не содержащая ни одной из этих n – 3 точек.

Решение:

Пусть X — произвольное множество из n – 3 точек.
Очевидно, что в нашем множестве M есть точка x, не принадлежащая множеству X.
Соединим ее прямыми с остальными точками множества M.
По условию все эти прямые различны, поэтому их ровно n – 1.
Поскольку в множестве X менее n – 1 точки, одна из проведенных прямых не пересекает X.
Через эту прямую и оставшиеся (n – 2) точки множества M проведём (n – 2) плоскости.
Так как этих плоскостей по-прежнему больше, чем точек во множестве X, одна из них не пересекает X.
Эта плоскость и является искомой.

Задача 3.Существуют ли 10 различных целых чисел таких, что все суммы, составленные из 9 из них — точные квадраты?

Решение:

ответ: Да.Обозначим искомые числа и их сумму соответственно через x1, … ,x10 и S. Тогда
Следовательно, . Пусть nk = 3k (k = 1, … ,10).
Тогда сумма квадратов делится на 9. Ясно, что числа  удовлетворяют требованиям задачи.

Задача 4.В треугольник ABC вписана окружность, касающаяся сторон AB, AC и BC в точках C1, B1 и A1 соответственно.
Пусть K — точка на окружности, диаметрально противоположная точке C1, D — точка пересечения прямых B1C1 и A1K.
Докажите, что CD = CB1.

Решение:

Заметим, что CA1 = CB1 (как касательные, проведенные к вписанной окружности из одной точки).
Пусть окружность с центром в точке C и радиуса CA1 = CB1 пересекает прямую A1K в точке D1.
Мы должны доказать, что точки D и D1 совпадают, т.е. что точки D1, B1 и C1 лежат на одной прямой.
Прямая KA1 перпендикулярна A1C1 и, следовательно, параллельна биссектрисе BO.
Поэтому .
Угол C при вершине равнобедренного треугольника A1CD1 равен 180 – 2 •  ∠ OBA1 =  ∠ A +  ∠ C,
следовательно, ∠ B1CD1 =  ∠ A.В равнобедренных треугольниках D1CB1 и B1AC1 углы при вершинах равны.
Поэтому равны и углы при основаниях: ∠ D1B1C =  ∠ C1B1A.
Это и значит, что точки D1, B1, C1 лежат на одной прямой.

4,6(94 оценок)

Это интересно:

Хобби-и-рукоделие

14.09.2022

Как составить гранатомет своими руками: Подробная инструкция...

Образование-и-коммуникации

05.03.2022

Как эффективно учиться: советы для успешного обучения...

Компьютеры-и-электроника

02.02.2022

Как создать файл в формате PDF с помощью бесплатного приложения OpenOffice...

Дом-и-сад