Вычисляем определитель матрицы 3×3:
∆ =
2 3 2
5 1 4
1 6 7
= 2·1·7 + 3·4·1 + 2·5·6 - 2·1·1 - 2·4·6 - 3·5·7 = 14 + 12 + 60 - 2 - 48 - 105 = -69.
Находим определители:
∆1 =
5 3 2
1 1 4
0 6 7
= 5·1·7 + 3·4·0 + 2·1·6 - 2·1·0 - 5·4·6 - 3·1·7 = 35 + 0 + 12 - 0 - 120 - 21 = -94.
∆2 =
2 5 2
5 1 4
1 0 7
= 2·1·7 + 5·4·1 + 2·5·0 - 2·1·1 - 2·4·0 - 5·5·7 = 14 + 20 + 0 - 2 - 0 - 175 = -143.
∆3 =
2 3 5
5 1 1
1 6 0
= 2·1·0 + 3·1·1 + 5·5·6 - 5·1·1 - 2·1·6 - 3·5·0 = 0 + 3 + 150 - 5 - 12 - 0 = 136.
ответ: x = ∆1 / ∆ = -94 / -69 = 94 / 69.
y = ∆2 / ∆ = -143 /-69 = 143 / 69.
z = ∆3 / ∆ = 136 / -69 = - 136 / 69.
1) Пусть х - наибольшее двузначное натуральное число, которое при делении как на 6, так и на 8 дает в остатке 15.
Тогда число х можно представить так:
х=6n+15
х=8m+15
Приравняем правые части и получим:
6n+15=8m+15
3n=4m
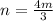
Так как n и m - натуральные числа, то возможные значения числа m это числа, кратные 3, точнее 3; 6; 9; 12;...
1) Пусть m=3, тогда
x= 8*3+15=24+15=39 - двузначное
2) Пусть m=6, тогда
x= 8*6+15=48+15=63 - двузначное
3) Пусть m=9, тогда
x= 8*9+15=72+15=87 - двузначное
4) Пусть m=12, тогда
x= 8*12+15=96+15=111 - трехзначное
Получается, что 87 - наибольшее двузначное натуральное число, которое при делении как на 6, так и на 8 дает в остатке 15.2) 100
2) 100 - наименьшее трехзначное натуральное число.
3) 100 - 87 = 13
На 13 число 87 меньше числа 100.
ответ: 13.