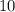 а два черных шара -
а два черных шара - 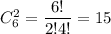 По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)
По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)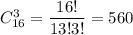
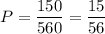
 И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно
И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно 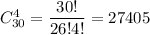

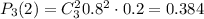
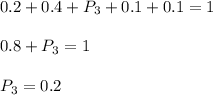


 а два черных шара -
а два черных шара - 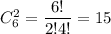 По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)
По правилу произведения, вынуть один белый шар и два черных шара можно кол-во благоприятных событий)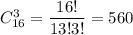
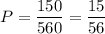
 И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно
И тогда выбрать делегацию из четырёх человек(1 мужчина и 3 женщин) можно 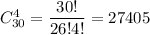




Входные данные:
{(a '(b)) / b - a (b) ^ 2 - cos (2 b) = 0, a (0) = -4}
Уравнение Риккати:
a '(b) = ba (b) ^ 2 + b cos (2 b)
Альтернативные формы:Больше
{a (b) ^ 2 + cos (2 b) = (a '(b)) / b, a (0) = -4}
{(a '(b) - ba (b) ^ 2 - b cos (2 b)) / b = 0, a (0) = -4}
{- (- a '(b) + ba (b) ^ 2 + b cos (2 b)) / b = 0, a (0) = -4}
Альтернативная форма, предполагающая, что b является положительным:
{b (a (b) ^ 2 + cos (2 b)) = a '(b), a (0) = -4}
Пошаговое объяснение: