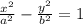 .
.
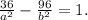

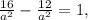
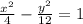
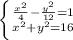
1. -3/6a - 4/6b
2. c - 1 9/12d
3. 2,6n - 3m
4. -5 1/14k - 15 1/5p
5. 3x - 1,8
6. 20,8
Пошаговое объяснение:
1. 1/3a + 2/3b - 5/6a - 1 1/3b = 2/6a + 4/6b - 5/6a - 1 2/6b = -3/6a - 4/6b
2. 2/3c + 0,5d + 2/6c - 2 1/4d = 8/12c + 6/12d + 4/12c - 2 3/12d = c - 1 9/12d
3. -2,5m + 4n - 1/2m - 1,4n = -2,5m + 2,6n - 0,5m = 2,6n - 3m
4. -12p + 1/7k - 5 3/14k - 3 1/5p = -15 1/5p + 2/14k - 5 3/14k = -5 1/14k - 15 1/5p
5. 4/5x - 1,8 + 5x - 2,8x = 5 8/10x - 2 8/10x - 1,8 = 3x - 1,8
6. 5,6y + 10,4 - 2 3/5y + 6,3 - 3y + 4,1 = 2,6y + 20,8 - 2,6y = 20,8
2х = 86 - 12
2х = 74
х = 74:2
х = 37
х+12=49
ответ: 49 мальчиков участвовало в олимпиаде.