Пошаговое объяснение:
Область определения:(– ∞ ;–1)U(–1;1)U(1;+ ∞ )
х=–1
Находим предел слева:
limx →–1–0f(x)=(1)/(–1–0)2–1)=– ∞ , так как
положительное число в числителе делится на очень маленькое в знаменателе.
Получим очень большое отрицательное (– ∞ )
Если функция имеет бесконечный предел в точке ( хотя бы один или слева или справа), то
Значит х=–1 – точка разрыва второго рода
Аналогично
х=1 – точка разрыва второго рода.
На
(– ∞ ;–1)
на
(–1;1)
на
(1;+ ∞ )
функция непрерывна как частное непрерывных функций:1 и x4–1
на отрезке [0;2]
имеет точку разрыва второго рода х=1
на отрезке [–3;1]
имеет точку разрыва второго рода х=–1
на отрезке [4;5] ∈ (1;+ ∞ ) непрерывна
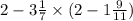
Сначала для удобства переведём дроби в неправильные:
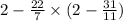
Теперь поочерёдно начнём выполнять действия. Первым действием является скобка. Перед тем, как выполнить вычитание, нужно привести оба числа в одинаковому знаменателю, для этого умножим 2 на 11 и после этого вычтем:
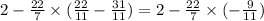
Следующим действием является умножение. Обе дроби являются отрицательными, значит их произведение будет положительным, так как при умножении минуса на минус бужет плюс. Сократим и умножим:
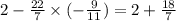
Осталось выполнить последнее действие, которым является сложение. Для начала приведём эти числа к общему знаменателю, сложим и выделим целую часть:
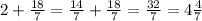
Вот и ответ.
(a-b)c=ab-ac
представим 98 как разность чисел 100 и 2
98=100-2
98*14=(100-2)*14=100*14-2*14=1400-28=1372