В равностороннем треугольнике ABC на сторонах AC и BC отметили точки D и E такие, что CD=2AD, BE=2CE. Обозначим точку пересечения отрезков AE и BD через F. Чему равен угол BFC?
Пошаговое объяснение:
1) Введем прямоугольную систему координат .Пусть АВ=ВС=АС=1. Пусть FC∩АВ=Р .Пусть ЕК⊥АС, ВН⊥АС, РМ⊥АС.
2) Определим координаты точек .
А(0;0) ,В(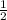
;
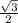) ,С(1;0) ,Н(0,5 ;0) ,D( 
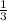;0) ,К( 
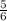;0) , Е(
3)Найдем координаты направляющих векторов: DB(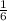 
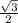; ) , РС( 
;
).
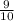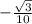4)Найдем скалярное произведение векторов .
DB *РС= * + *( ) =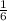
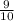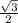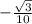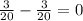⇒вектор DB⊥PC ⇒∠BFC=90°.
=======================================
Пояснения( жуткие вычисления , слабонервным можно не читать).
1) Координаты точки Е. ΔКСЕ прямоугольный .
КЕ=СЕ*sin60= *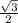 
.
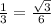КС=СЕ*cos60=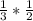 
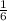= , поэтому АК= 1-
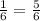→ Е( ;
) .
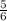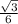2)Координаты точки В. ΔАВН- прямоугольный .
АН=НС= .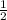
ВН=АВ*sin60=1* =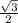
3)Ищем координаты точки Р
а)ΔВDC , по т. Менелая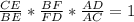 
, 
, 
.
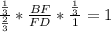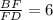б)ΔАВD , по т. Менелая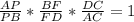 
, 
, 
,
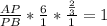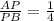AP=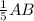
= 
.
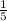в)ΔАРМ прямоугольный .
РМ=АР*sin60= * =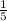 
.
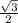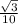АМ=АР*cos60=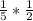 
=
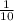→ P ( ; ) .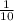
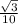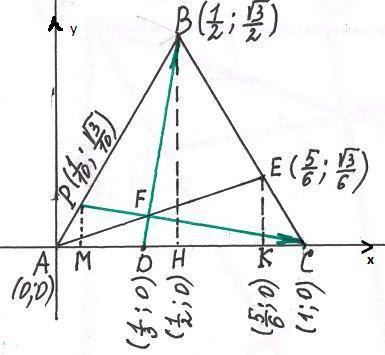
Пусть скорость мотоциклиста из пункта А до В равна х км/ч
весь путь вычисляется по формуле
S=vt
Тогда время в часах затраченное мотоциклистом от А до В равно
t = S/x
а время от В до А равно
S/2÷ (x+9)+S/2÷30
так как время обратного пути мотоциклиста равно первоначальному, то получаем следующее уравнение
S/x = S/2÷ (x+9)+S/2÷30
Делим обе части уравнения на S, т.к. знаем, что S, не равно 0
переносим в одну сторону. Получаем следующее уравнение
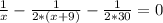
приведем к общему знаменателю
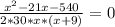
Дискриминант равен (-21)²-4*1* (-540)= 2601
Д больше 0, значит уравнение имеет 2 корня
Так как скорость не может быть отрицательным числом, значит
ответ 36 км/ч
2)45см >40см
3)212см> 210см