Для поиска корня уравнения 19 - 2(3x + 8) = 2x - 37 используем тождественные действия, так как они используются для нахождения корней линейных уравнений.
Применим для открытия скобок два правила.
1. Дистрибутивный закон умножения: a * (b + c) = a * b + a * c;
2. Как выполнить открытие скобок перед которой стоит минус.
19 - 2(3x + 8) = 2x - 37;
19 - 2 * 3x - 2 * 8 = 2x - 37;
19 - 6x - 16 = 2x - 37;
Группируем подобные в разных частях:
-6x - 2x = -37 - 19 + 16;
-8 * x = -40;
x = -40 : (-8);
x = 5.
Пошаговое объяснение:
Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
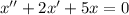
Используя замену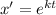 
, получим характеристическое уравнение
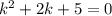
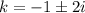
Общее решение однородного дифференциального уравнения:
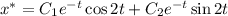
Рассмотрим функцию: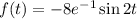 
. Здесь 
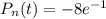откуда 
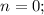и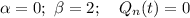 
. Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
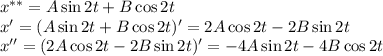
Подставляем в исходное дифференциальное уравнение:
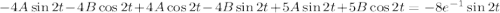
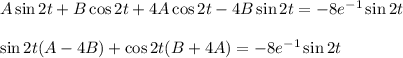
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
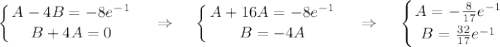
Общее решение линейного неоднородного дифференциального уравнения:
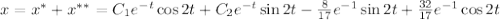
Осталось решить задачу Коши, подставляя начальные условия
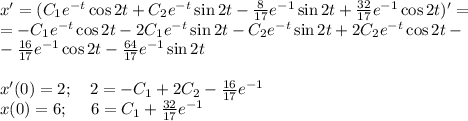
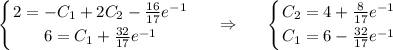
Частное решение задачки Коши:
2)326+92=418
3)582+418=1000