S = V * t, где t - оптимальное время.
1. Найдем оптимальное время.
S1 = V1 * t1, где V1 = 10км/ч, t1 = t-1 (на час раньше оптимального),
S2 = V2 * t2, где V2 = 5км/ч, t2 = t+1 (опоздание на час от оптимального)
1) S1 = 10(t-1)
2) S2 = 5(t+1)
Учитывая, что в первом и во втором случаях расстояние, преодолеваемое Шеком, одинаковое, тогда справедливо равенство: S1 = S2. Выразим это равенство путем подстановки сведений о скорости и времени для двух случаев.
10 ( t - 1 ) = 5 ( t + 1 )
10t - 10 = 5t + 5
10t - 5t = 5 + 10
5t = 15
t = 3 часа
Вывод: 3 часа оптимальное время для Шрека, за которое он должен преодолеть расстояние S, чтобы прибыть в замок своевременно.
2. Определим расстояние S.
Во всех рассматриваемых случаях расстояние одно и то же. Следовательно справедливы равенства: S = S1 = S2. Для расчета расстояния S возьмем одну из расчетных формул для S1 или S2, записанных выше. Вместо оптимального времени t подставим найденные ранее 3час. Например, берем формулу для S1.
S1 = 10 (t - 1) = 10(3 - 1) = 10 * 2 = 20км.
S1 = 20км.
Вывод: расстояние до замка, которое Шрек преодолеет, равно 20 км.
3. Теперь, зная расстояние и оптимальное время, можно рассчитать оптимальную скорость (при желании). Расчет осуществляется по формуле:
V = S : t, где S=20км, t=3час.
(у - х)(у+х+ху)
Пошаговое объяснение:
- 
+ x - y = ( - ) + (x - y) = (y - x)(y + x) + xy(y - x) = (y - x)(y + x + xy)
1) Существует несколько разложения многочленов на множители, среди них: вынесение общего множителя за скобку, группировки, применение формул сокращённого умножения. В данном задании в первую очередь применяем группировки: первое группируем со вторым, третье - с четвёртым.
2) Первую скобочку - разложили на множители по формуле сокращённого умножения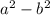 
= (a - b)(a + b), из второй (x - y) выносим общий множитель ху
3) Видим, что у нас образовалась одинаковая скобка, (у - х), выносим её, как общий множитель за скобку, остальное всё (то, что осталось) переписываем во вторую скобку. В левой части (до знака + ) осталось у + х, в правой ху.
