ответ: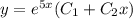
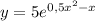
Пошаговое объяснение:
Определить общее решение дифференциального уравнения:
y" - 10y' + 25y = 0.
Решение
Характеристическое уравнение имеет вид:
k² - 10k + 25 = 0
(k - 5)² = 0
k₁ = k₂ = 5
Корни действительные и равные k₁ = k₂ = k . В этом случае общее решение уравнения:
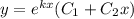
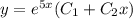
Определить частное решение дифференциального уравнения:
y'+y=xy, удовлетворяющее начальному условию y(2)=5.
Решение
y' + y = xy
y' = xy - у
Делим обе части уравнения на у
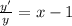
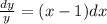
Интегрируем обе части уравнения
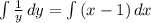
ln|y| -lnC = 0.5x² - x
Запишем общее решение ДУ
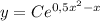
Найдем частное решение ДУ подставив начальные условия y(2)=5
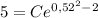
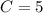
Поэтому частное решение ДУ
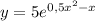
2)сенын
сіздін
3)онын