Пошаговое объяснение:
1)Решите графически систему уравнений.Выполните проверку,подставив найденные решения в уравнения системы :
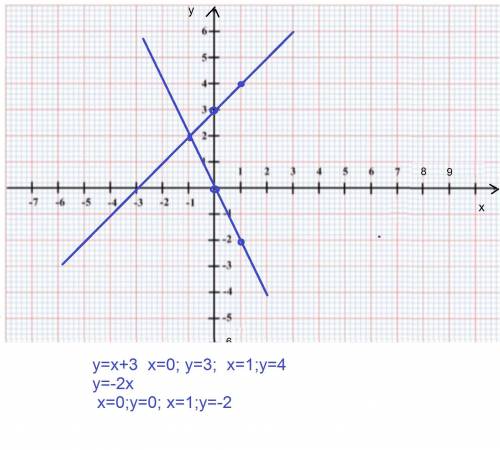
графиком линейных функций являются прямые линии их можно построить по двум точкам
у=х+3 х=0; y=3; x=1;y=4
у=-2х x=0;y=0; x=1;y=-2
графики пересекаются в точке (-1;2)
проверка
-1+3=2
-1*(-2)=2 верно
2)Решите систему подстановки:
у=3-х
4х-у=12 4х-(3-х)=12; 4x-3+x=12; 5x=15; x=3; y=3-3=0; y=0
3) Не выполняя построений,найдите координаты точки пересечения графиков уравнений:
2х+3у=0
х-2у=28 умножим на -2
2х+3у=0
-2х+4у=56 сложим оба уравнения
7у=56; y=8; подставим в первое уравнение 2х+24=0 ;x=-12
(-12;8)
(x²-3x-4)(x²-7x+12)≤0
1) x²-3x-4=0
x₁=-1; x₂=4 (a-b+c=0 [1+3-4=0], x₁=-1; x₂=-c/a=4/1=4)
2) x²-7x+12=0
D=(-7)²-4*12=49-48=1
x₁=(7+1)/2=8/2=4
x₂=(7-1)/2=6/2=3
(x+1)(x-4)(x-3)(x-4)≤0
(x+1)(x-3)(x-4)²≤0
(x-4)²≥0 при x∈R
(x+1)(x-3)≤0
+ - +
..
-3 1
x∈[-3;1]
ответ: x∈[-3;1]