Прямая АС и ось цилиндра ОО1 лежат в разных плоскостях и не пересекаются. Они скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. При этом получатся пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися.
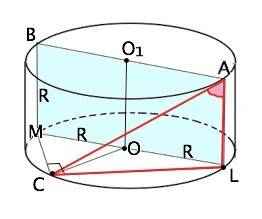
Осевое сечение цилиндра - прямоугольник, перпендикулярный основаниям. Его сторона АL параллельна оси ОО1.
⇒ угол САL- искомый.
∆ МОС равнобедренный (образован радиусами), его центральный угол МОС=60° (равен дуге МС), поэтому углы при основании МС равны по 60°
Вписанный угол МСL, как опирающийся на диаметр ML , равен 90°. => ∆ МСL- прямоугольный.
СL=ML•sinСML
СL=2R•sin60°=2R•√3/2=R√3
tg∠LАC=CL:AL=R√3/R=√3 – это тангенс 60°
Угол между прямой АС и осью цилиндра равен 60°
12²=144
13²=169
14²=196
15²=225
16²=256
17²=289
18²=324
19²=361
20²=400