Москва 168 км Тверь Санкт-Петербург
> 74 км/ч t = 7 ч > х км/ч
по действиям).
1) 168 : 7 = 24 (км/ч) - скорость сближения;
2) 74 - 24 = 50 (км/ч) - скорость грузовой машины.
Выражение: 74 - 168 : 7 = 50.
по действиям).
1) 74 · 7 = 518 (км) - проедет легковой автомобиль за 7 часов;
2) 518 - 168 = 350 (км) - проедет грузовой автомобиль за 7 часов;
3) 350 : 7 = 50 (км/ч) - скорость грузового автомобиля.
Выражение: (74 · 7 - 168) : 7 = 50.
уравнение).
Пусть х (км/ч) - скорость грузовой машины, тогда (74 - х) км/ч - скорость сближения. Уравнение:
(74 - х) · 7 = 168
74 - х = 168 : 7
74 - х = 24
х = 74 - 24
х = 50
ответ: 50 км/ч.
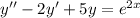
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является 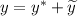 .
.
1) 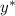 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
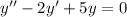
Применим метод Эйлера: сделаем замену 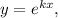 где
где 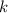 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 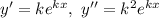
Получили характеристическое уравнение:
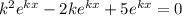
Разделим обе части уравнения на 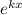 :
:
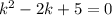
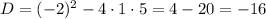
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
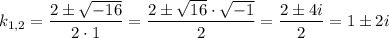
Тогда 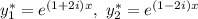
Воспользуемся формулой Эйлера: 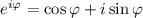
Фундаментальная система решений: 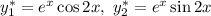 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 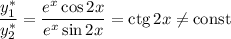
Общее решение: 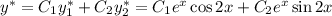
2) 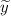 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 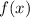 .
.
Здесь 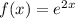 , причем
, причем 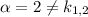 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 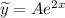 , где
, где 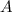 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда 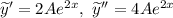 и
и 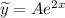 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 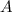 :
:
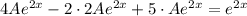
Разделим обе части уравнения на 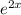
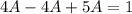
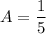
Таким образом, частное решение: 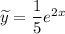
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
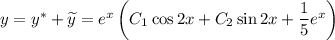
ответ: 
Никита съел половину последнего остатка и последний блинчик, значит
1 блин - половина последнего остатка,значит для Никиты осталось 1+ 1 = 2 блина
2 блина оставил Максим, а съел он 2 + 1 = 3 блина - что является половиной от оставленных ему Ирой блинов, тогда Максим съел 3 + 1 = 4 блина
Ира оставила ребятам 2 + 4 = 6 блинов
считаем 6 + 1 = 7 блинов - половина порции Иры, тогда 7*2 14 блинов пожарила тётя Нюра