1) Дано:
sin a = 0,8
90° ≤ a ≤ 180°
Найти: cos a, tg a, ctg a
Решение: Воспользуемся основным тригонометрическим тождеством sin²a+cos²a = 1
и выразим косинус cos a = √(1- sin²a).
Т.к. 90° ≤ a ≤ 180°,то косинус будет отрицательным
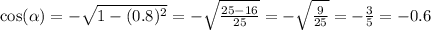
Из-за отрицательного косинуса и тангенс, и косинуса тоже будут отрицательными
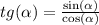

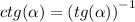

2) Дано:
tg a =4/3
180° ≤ a ≤ 270° (т.к. тангенс положительный только в 1 и 3 четвертях)
Найти: tg 2a, ctg 2a
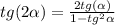
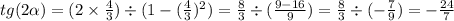
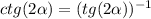
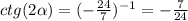
3) Дано:
sin a = 0,1
270° ≤ a ≤ 360°
Найти: cos a
Решение: Воспользуемся основным тригонометрическим тождеством sin²a+cos²a = 1
и выразим косинус cos a = √(1- sin²a).
Т.к. 270° ≤ a ≤ 360°,то косинус будет положительным
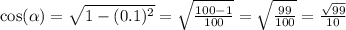
Найдите длины сторон треугольника ABC, если известно, что AB так относится к BC, как 7 к 4, BC так относится к AC, как 6 к 5, а его периметр равен 64,5.
По условию задачи: АВ: ВС=7:4, значит АВ= 7*ВС: 4
ВС: АС=6:5, значит АС=5*ВС: 6
Р= АВ+ВС+АС=64,5
Подставим в выражение АВ и АС:
7*ВС: 4 + 5*ВС: 6 + ВС= 64,5 (лучше дробью записывать)
(21* ВС+10 * ВС): 12 + 12*ВС: 12=64,5
43*ВС=64,5*12=74
ВС=18
Теперь найдем другие стороны:
АС= 5*18:6=15
АВ=7*18:4=31,5