12 см - длина меньшей стороны прямоугольника
Пошаговое объяснение:
Пусть меньшая сторона = х см, тогда большая сторона = х+2 см
S = a*b, где S = 168 см², a - длина = (х+2) см и b - ширина = х см
Составим уравнение:
(х+2)*х = 168
х² + 2х = 168
х² + 2х - 168 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 2² - 4·1·(-168) = 4 + 672 = 676
Так как дискриминант больше нуля, то квадратное уравнение имеет два действительных корня:
x₁ = (-2 - √676)/(2·1) = (-2 - 26)/ 2 = -28/2 = -14 - не подходит, отрицательное число
x₂ = (-2 + √676)/(2·1) = (-2 + 26)/2 = 24/2 = 12 (см) - длина меньшей стороны прямоугольника
168 : 12 = 14 (см) длина большей стороны
14 - 12 = 2 (см) одна из сторон меньше другой на 2 см
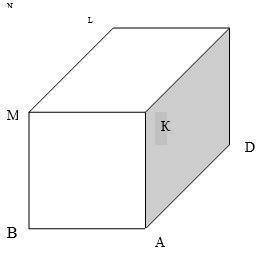
1. CLND, BMLC, ABCD
2. MN = 3√5 см
NL = 3 см
DL = 5 см
3. Рис. 2. (начерти на листе в клетку (1 клетка на листе = 5 мм, я изобразил наглядно, 1 клетка = 1 см)
4. ABMK = DCLN = 12 см²
ADNK = BCLM = 24 см²
MLNK = ABCD = 18 см²
5. S = 108 см²
Объяснение:
Решения:
1. CLND, BMLC, ABCD
2.
a) MN²=MK²+KN²
MK = AB = 3 см
KN = AD = 6 см
MN² = 3² + 6² = 9 + 36 = 45
MN = √45 = √(9*5) = √(3²*5) = 3√5
MN = 3√5 см
б) NL = AB = 3 см
NL = 3 см
в) DL²=DC²+CL²
DC = AB = 3 см
CL = AK = 4 см
DL² = 3² + 4² = 9 + 16 = 25
DL = √25 = 5
DL = 5 см
3. Рис. 2
4. ABMK = DCLN = 4*3 = 12 см²
ADNK = BCLM = 4*6 = 24 см²
MLNK = ABCD = 3*6 = 18 см²
5. S поверхности параллелепипеда = 12*2 + 24*2 + 18*2 (сумма всех граней) = 24 + 48 + 36 = 108 см²
S = 108 см²
объяснение:10÷5×2
12÷4×3=9