постоянный положительный множитель можно выносить за знак модуля, поэтому уравнение примет вид:
|x+1|-|x-2|+3|x+2|=5
Универсальный метод решения уравнений с модулями - метод интервалов (метод расщепления)
Найдем нули подмодульных выражений:
x+1=0 => x=-1
x-2=0 => x=2
x+2=0 => x=-2
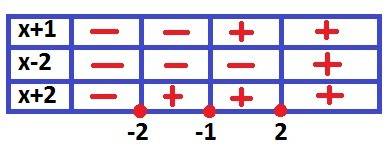
Составим небольшую таблицу, по которой определим знак каждого промежутка с пробной точки (см. рисунок)
Если в промежутке стоит +, то модуль просто опускается, если же -, то знаки под модулем меняются на противоположные
1 случай)
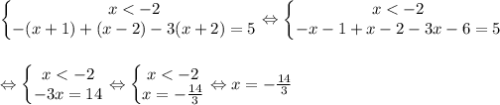
2 случай)
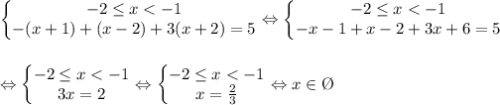
3 случай)
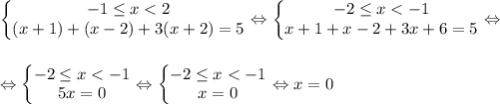
4 случай)
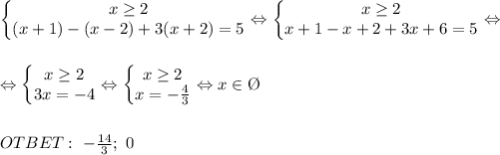
y = x⁵ - 10x³ - 135x
y' = 5x⁴ - 30x² - 135 по правилу (xⁿ)' = n * xⁿ⁻¹
Находим точки экстремума:
5x⁴ - 30x² - 135 = 0
Замена x² = t
5t² - 30t - 135 = 0 | :5
t² - 6t - 27 = 0
t₁ = 9, t₂ = -3
Обратная замена:
x² = 9 ⇒ x = -3, x = 3
x² = -3 -- не имеет действительных корней
x = 3 не принадлежит отрезку [-5; 0]. Подставляем в функцию y(x) значения -5, -3, 0:
y(-5) = (-5)⁵ - 10*(-5)³ - 135*(-5) = -3125 + 1250 + 675 = -1200
y(-3) = (-3)⁵ - 10*(-3)³ - 135*(-3) = -243 + 270 + 405 = 432
y(0) = 0⁵ - 10*0³ - 135*0 = 0 - 0 - 0 = 0
432 > 0 > -1200 ⇒ Наибольшее значение функции на отрезке [-5; 0] равно 432
1)4.2/9+3.4/9=7.6/9
2)7.6/9-6.5/9=1.1/9
3-2.3/11+2.5/11= -1.8/11
1)2.3/11+2.5/11=4.8/11
2)3-4.8/11= -1.8/11
(8.1/8-5.7/8)+2.5/8=4.7/8
1)8.1/8-5.7/8=2.1/4
2)2.1/4+2.5/8=4.7/8