а) 3x^2+40x+10<-x^2+11x+3
4x^2+29+7=0
D=841-112=729
x1=-7
x2=-0.25
x принадлежит (-7:-0,25)
б)сразу раскрываю
15х^2+3x-5x-1>4x62-x+8X-2
11x^2-9x+1
D=81-44=37
x1=9-корень из 37/ 22
x2=9+корень из 37 / 22
X принадлежит (-бесконечность:9-корень 37/22)(9+корень из 37/22)
А) 5x^2>2x
5x^2=2x
5x^2-2x=0
x(5x-2)=0
x=0 или x=0.4 x принадлежит (-бесконечность:0)(0.4 : + бесконечность)
б)-0.3x<0.6x^2
0.6x^2+0.3x=0
x(0.6x+0.3)=0
x=0 или х=-0.5
x принадлежит от (- бесконечность: -0.5)(0: + бесконечность)
Пусть x овощей имеют массу меньше 1000, y - больше 1000, а z - ровно 1000.
а) Предположим, что да. Тогда справедливо уравнение:
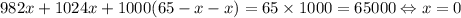, но x очевидно не может быть нулем, т.к. среднее арифметическое больше нуля. Противоречие.
б) Предположим, что это возможно. Тогда x+y+13=65 ⇔ x+y=52. Аналогично строим уравнение: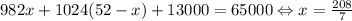 
, получили противоречие: x должно быть целым числом.
в) Понятно, что минимальная масса встречается только в группе, где расположены овощи массой меньше 1000 г. Обозначим массу самого легкого за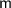 
; Пусть масса оставшихся в этой же группе овощей суммарно равна 
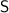; Тогда 
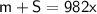; Заметим, что 
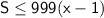; Поэтому 
(*);
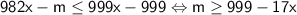Теперь рассмотрим уравнение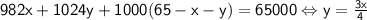 
, значит x кратно 4. Пусть 
;
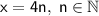Рассмотрим другое уравнение: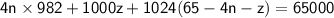 
; Отсюда получаем, что 
;
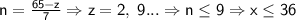Возвратимся к (*):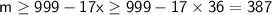 
; Приведем пример при котором осуществима оценка:
Пусть в первой группе 1 овощ весит 387 граммов, а остальные 35 весят по 999 граммов. Во второй группе 2 овоща весят по 1000 граммов. А в последней группе 27 овощей весят 1024 грамма.
ответ: а) нет
б) нет
в) минимально возможная масса - 387 граммов
Тогда соседние ему числа, это 21 и 23 (нечетные), теперь считаем до следующего чётного (если надо). А так, только соседние.