
1. 8Х + 10 = 3Х - 10
8Х - 3Х = - 10 - 10
5Х = - 20
Х = - 20 : 5
Х = - 4
ответ: Х = - 4
2. 10 * (У - 2) - 12 = 14 * (У - 2)
10У - 20 - 12 = 14У - 28
10У - 14У = 20 + 12 - 28
- 4У = 4
У = 4 : (- 4)
У = - 1
ответ: У = - 1
3. - 25 * (- 8Х + 6) = - 750
200Х - 150 = - 750
200Х = - 750 + 150
200Х = - 600
Х = - 600 : 200
Х = - 3
ответ: Х = - 3
4. - 10 * (- 4Х + 10) = - 300
40Х - 100 = - 300
40Х = - 300 + 100
40Х = - 200
Х = - 200 : 40
X = - 5
ответ: Х = - 5
5. 3 * (5У - 6) = 16У - 8
15У - 18 = 16У - 8
15У - 16У = - 8 + 18
- У = 10
У = - 10
ответ: У = - 10
6. - 5 * (3Х + 1) - 11 = - 1
- 15Х - 5 - 11 = - 1
- 15Х = - 1 + 5 + 11
- 15Х = 15
X = 15 : ( - 15)
Х = - 1
ответ: Х = - 1
7. - 8У + 4 = - 2 * (5У + 6)
- 8У + 4 = - 10У - 12
- 8У + 10У = - 12 - 4
2У = - 16
У = - 16 : 2
У = - 8
ответ: У = - 8
8. 20 + 30Х = 20 + Х
30Х - Х = 20 - 20
29Х = 0
X = 0 : 29
Х = 0
ответ: Х = 0
9. 26 - 5У = 2 = 9у
14У = 24
У = 24 : 14
У = 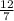 ≈ 1.71428571428571
≈ 1.71428571428571
ответ: У = 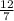 ≈ 1.71428571428571
≈ 1.71428571428571
Вот Так!
а) Если чисел выписано 7, то их было задумано 3. Их не могло быть меньше (у двух чисел сумм выписывается всего 3), и не могло быть больше (у четырёх чисел сумм будет 15). Нуля в наборе нет, а есть положительные и отрицательные числа. Какое-то встречается один раз, а какое-то два. Если отрицательное число одно, то положительных два, но тогда из них формируются три положительные суммы. Значит, было два отрицательных числа и одно положительное число, равное 7. Из отрицательных чисел может быть сформировано -5, чтобы в сумме с 7 получалось 2. Сумма же отрицательных чисел равна -13. Значит, это числа -8 и -5. А весь набор задуманных чисел был такой: -8, -5, 7. Легко видеть, что этот вариант подходит.
б) Пример с пятью числами: -2,-1,0,1,2. Легко проверяется, что выписано будет 31 число, где ±3 появляется 2 раза, ±2 -- 4 раза, ±1 -- 6 раз, и 0 появится ровно 7 раз. Четырёх различных чисел недостаточно. Это легко проверяется, так как 0 сам по себе встречается не более одного раза, среди пар он встречается не более двух раз (пары с одинаковой суммой не пересекаются), среди троек не более одного раза (все их суммы различны), и как сумма всех чисел тоже не более одного раза -- итого получается меньше семи.
в) Нет, не всегда. Пусть задуманы числа 1, 2, -3. Из них формируется набор чисел от -3 до 3 (без повторений). Ясно, что если у всех задуманных чисел сменить знак, то получится то же самое, поэтому задуманы могли быть и числа -1, -2, 3.