Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.
Правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше
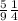
общий 36
первую дробь домножаем на 4,вторую на 9
привели и сравниваем, получается,что
5\9=20\36,1\4=9\36
20\36>9\36 => 5\9>1\4
Пошаговое объяснение:
Задать вопрос
Войти
Решить уравнение: |x|=7; |x|=-4; -(-x)=-25.
1) |x|=7. Поскольку модуль числа для положительного числа и нуля равен самому числу, а для отрицательного — противоположному числу. То раскрыв знак модуля имеем: 2 случая: 1) При х< 0 => x1 = -7; 2) при x>=0 => x2 = 7.
2) |x| = -4. Поскольку модуль числа n - это расстояние от начала координат до точки n, то значение модуля не может быть отрицательным числом, поэтому уравнение |x| = -4 не имеет решений.
3) -(-x) = -25. Разделим обе части уравнения на -1, получим: -x = 25, х = -25. Проверка: -(-(-25)) = -25, -25 = -25.
2) с + d
3) a-b + c+d