
Пошаговое объяснение:
Пошаговое объяснение:
1) сначала докажем что AB параллельно CD:
вектор AB=(1;-1), CD=(-1,1), CD=-AB => параллельны
2) докажем BC параллельно AD
вектор BC = (-1, -1), AD = (-1;-1), вектора равны BC=AD => параллельны
AB параллельно CD и BC параллельно AD => ABCD - параллелограмм
3) докажем равенство сторон
вектор CD=-AB => стороны равны CD=AB
длина AB = 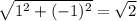
вектор BC=AD => стороны BC=AD
длина BC = 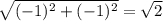
ABCD - параллелограмм и длины сторон равны => ABCD - ромб
4) докажем угол BAD - прямой
произведение векторов
AB*AD = (1;-1) * (-1; -1) = 1*(-1) + (-1)*(-1) = -1+1=0
AB перпендикулярно AD
ABCD - ромб, BAD - прямой => ABCD - квадрат
ответ:
пошаговое объяснение:
полное решение составляется из 2:
1) общее решение однородного уравнения т.е. уравнения y"+9y=0
2) и частного решеня неоднородного (т.е. того что вы написали)
для нахождения общее решение
однородного уравнения запишем характеристическое уравнение
k^2+9=0 => k=3 и k=-3
тогда общее решение однородного уравнения запишется так a*e(3x)+b*e(-3x)
частного решеня неоднородного будем
искать в виде(в виде правой части нашего уравнения)
y= c*e(3x)
найдем y"
y'= c*3*e(3x) y"= c*9*e(3x)
подставим в уравнение получим
c*9*e(3x) + 9*c*e(3x) = 6*e(3x) ==> c*9 + 9*c = 6 ==> 18*c=6 ==> c=6/18=1/3
полное решение будет
y = a*e(3x)+b*e(-3x) +1/3*e(3x)
=(a+1/3)*e(3x)+b*e(-3x)
подробнее - на -