Так как в задаче нет точных чисел, мы возьмём любые.
Допустим сделаем задачу так:
У Васи 20 рублей, это в 3 раза меньше чем у Пети, а у Толика — в два раза больше, чем у Пети и Васи вместе. Сколько всего денег было у всех ребят вместе?
Решение задачи устно:
Мы не знаем сколько рублей у Пети, но в условиях было сказано: что у Васи 20 рублей, это в 3 раза меньше чем у Пети. Значит мы двадцать должны умножить на три (20*3), получается шестьдесят (60). Теперь мы можем узнать сколько денег у Пети и Васи вместе. То есть двадцать складываем с шестьдесят (20+60), получается восемьдесят (80). После этого нам нужно узнать: сколько рублей было у Толика. Мы должны восемьдесят умножить на два (80*2. Чтобы было не сложно считать, вспомните таблицу умножения на 8, то есть сколько будет 8*2. Это как 80*2, только 80 без нолика. 8*2 получается 16. Такой же ответ получается в примере 80*2, только прибавляем нолик к 6. получается 160.), получается 160. А теперь мы должны узнать сколько денег всего было у всех ребят. Сколько у Пети и Васи всего рублей мы уже знаем (80 рублей), значит мы должны сколько теперь станет если прибавить деньги Толика. То есть восемьдесят складываем со сто шестьдесят, то и получается у нас двести сорок. Значит ответ у нас: всего 240 рублей было у всех ребят вместе?
Решение действиями:
1) 20*3=60 (руб.)- было у Пети.
2) 60+20=80 (руб.)- у Пети и Васи вместе.
3) 80*2=160 (руб.)- было у Толика.
4) 160+80=240 (руб.)
Всего 240 рублей было у всех ребят вместе?
Надеюсь ты этого хотел(а) :D
Это показательное уравнение вида 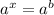 , где
, где 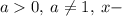 неизвестная переменная.
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения 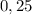 представить в виде числа со степенью так, чтобы в основании было число
представить в виде числа со степенью так, чтобы в основании было число 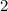 . Это явно число
. Это явно число 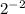 (проверка:
(проверка: 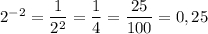 ).
).
Значит теперь, когда наше показательное уравнение имеет вид 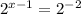 , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение 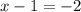 после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е.
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 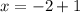 .
.
Из этого следует, что ответ нашего показательного уравнения равен 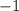 .
.

полгода это 1/2 года т.е. не 10 процентов а 5
300*5=1500
30 000+1500=31 500