x + y + z + t = 3.571335
Пошаговое объяснение:
Вычтем превое уравнение из второго. После преобразований получим:
(t - x)(yz + y + z) + t - x = 2
Теперь умножим первое уравнение на t, второе на x и вычтем из первого второе.
Получим после преобразований:
(t - x)(yz + x + y) = t - 3x.
Комбинируя эти два уравнения, найдем
t - 2x =1.
Аналогично, для пар 2-го и 3-его, 3-его и 4-го, 4-го и 1-го уравнений находим:
2x - 3y = 1; 3y - 4z = 1; t - 4z = 3.
Только три из этих уравнений независимы. Чтобы найти решение, выразим
x, y, z через t
x = (t - 1)/2, y = (t - 2)/3, z = (t - 3)/4,
и подставим результат в 4-ое уравнение исходной системы.
После раскрытия скобок получим
t3 + 3t2 + 3t - 47 = 0, или
(t + 1)3 = 48.
Действительный корень этого уравнения один:
t = 481/3 - 1.
Выразим через t сумму x + y + z + t:
x + y + z + t = (25t - 23)/12;
После подстановки найдем приближенно:
x + y + z + t = 3.571335.
9216
Пошаговое объяснение:
Предположим, что существует несократимая дробь, наибольший общий делитель d числителя и знаменателя которой отличен от 1. Но тогда эту дробь можно сократить на d. Получили противоречие, а значит, числитель и знаменатель являются взаимно простыми. Поскольку у правильной дроби числитель меньше знаменателя, то для ответа на вопрос необходимо вычислить количество чисел, взаимно простых с 8! и не превышающих 8! Задача сводится к нахождению функции Эйлера φ от числа 8!
Воспользуемся свойством мультипликативности функции Эйлера:
если a и b — взаимно простые, то φ(ab) = φ(a)φ(b)
Замечу, что степени двух различных простых чисел (p_1)^α и (p_2)^β являются еще и взаимно простыми:
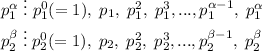
(видно, что у (p_1)^α и (p_2)^β нет общих делителей, кроме 1)
Исходя из изложенного, если записать каноническое разложение 8! на простые множители:
8! = 8×7×6×5×4×3×2×1 = 2³×7×2×3×5×2²×3×2 = 2^7 × 3² × 5 × 7,
то станет целесообразно упростить решение: φ(8!) = φ(2^7)φ(3²)φ(5)φ(7)
А теперь приведу формулу для вычисления φ(p^α) (p — простое):
φ(p^α) = p^α - p^(α-1)
Если же α = 1, то:
φ(p) = p-1
Имеем:
φ(8!) = φ(2^7 × 3² × 5 × 7) = φ(2^7)φ(3²)φ(5)φ(7) = (2^7 - 2^6)(3² - 3)(5-1)(7-1) = 2^6(2-1) × 3(3-1) × 4 × 6 = 64×3×2×4×6 = 9216,
что и есть ответ на вопрос задачи.
(Вот держи)