Сначала определения. Степень вершины графа - это количество рёбер, которые выходят из этой вершины. Петля - ребро, начало и конец которого находятся в одной и той же вершине. При подсчёте степени ребро-петля учитывается дважды.
а) 9, 8, 8, 7, 6, 6, 3, 2, 1
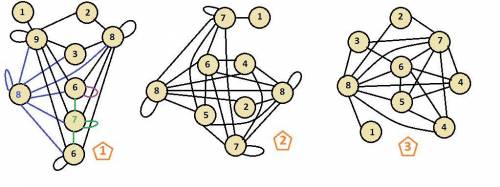
Количество вершин с нечётной степенью (9,7,3,1) чётное. Так как вершин всего 9, а старшая степень тоже равна 9, то без рёбер-петель не обойтись. Пример такого псевдографа на рис. 1
б) 8, 8, 7, 7, 6, 5, 4, 2, 1
Количество вершин с нечётной степенью (7,7,5,1) чётное. Так как вершин всего 9, старшая степень 8 у двух вершин, а младшая степень 1 только у одной вершины, то без рёбер-петель опять не обойтись. Пример такого псевдографа на рис. 2
в) 8, 7, 6, 5, 4, 4, 3, 2, 1
Количество вершин с нечётной степенью (7,5,3,1) чётное. Пример такого графа на рис. 3
г) 8, 7, 5, 4, 4, 3, 2, 2, 2
Количество вершин с нечётной степенью (7,5,3) нечётное. Такой граф построить нельзя, так как каждое ребро соединяет две вершины, поэтому сумма степеней вершин графа - число чётное.
ответ: а) б) в)